ЛЕКЦИОННОЕ ЗАНЯТИЕ. ДВОЙНОЙ ИНТЕГРАЛ, ЕГО ПРОСТЕЙШИЕ СВОЙСТВА. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ

 

8.1 Вычисление двойных интегралов базируется на
понятии повторного интеграла

Пусть рассматривается на плоской области и она правильная в направлении оси , т.е. всякая прямая, параллельная оси , пересекает границу области не более чем в двух точках. Тогда область удобно спроектировать на ось . Пусть проекция на есть .

Если – уравнение нижней границы, а – уравнение верхней границы, то любому области принадлежат те точки вертикального отрезка, которые удовлетворяют
неравенствам

(*)

Выражение вида называется повторным
интегралом от функции по области . Он вычисляется
следующим образом:

сначала находится внутренний интеграл (– переменная интегрирования, 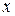– фиксированная), а затем полученную функцию аргумента 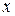интегрируем на .

Значение повторного интеграла – число.

Пример 1. Вычислить повторный интеграл ,
восстановив область .

Решение. Интеграл вычисляется по : (см. рисунок).

 

 

.

Аналогично:

если область – правильная в направлении оси , то ее удобно проектировать на ось . Пусть проекция области на ось есть отрезок , уравнение левой границы области , а правой границы – . Тогда для всякого значение 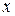точек прямой , принадлежащих области , удовлетворяет неравенствам . Поэтому область можно
задать в виде

(см. рисунок).

Такому заданию области соответствует повторный интеграл . Для его вычисления находится сначала внутренний интеграл, а затем внешний.
Результат – число!

Пример 2. Зададим область примера 1, проектируя ее на ось , Вычислить повторный интеграл .

Решение.

.

Замечаем, что значения различных повторных интегралов
функции по области оказались равными.

Доказано (см. [1]) утверждение:

если непрерывна на , ; область является
правильной в направлении осей координат, то значение двойного интеграла совпадает со значением соответствующего повторного интеграла, причем результат не зависит от порядка
интегрирования, т.е.

.