Лекционное занятие. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ, СОДЕРЖАЩИХ КВАДРАТНЫЙ ТРЕХЧЛЕН

Пример 10.

 

 

Рассмотрим интегралы следующих трех типов:

где или . Отметим, что интегралы 1-го и 2-го типа при возникают при интегрировании дробно-рациональных функций.

Укажем общие рекомендации по отысканию интегралов этих трех типов.

В интеграле выделить из квадратного трехчлена полный квадрат.

В интеграле выделить в числителе производную квадратного трехчлена.

В интеграле вынести 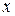из-под корня.

Пример 1. Найти интеграл .

Имеем интеграл первого типа при . Выделим из квадратного трехчлена полный квадрат: .

Используя это равенство и формулу (13) п.12.3, получим

Пример 2. Найти интеграл .

Имеем интеграл второго типа при . Найдем производную квадратного трехчлена и выделим ее в числителе следующим образом:

.

Тогда

Второй интеграл в этой сумме был найден в примере 1:

В первом интеграле воспользуемся тем, что

Обозначив , окончательно получим:

Пример 3. Найти интеграл .

Имеем интеграл третьего типа. Вынесем 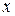из-под корня:

.

Воспользуемся тем, что ,

.

Используя эти равенства и формулу (12) п.12.3, получим

.