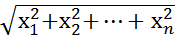Понятие n-мерного вектора
Правило Крамера для любой системы линейных уравнений.
(*)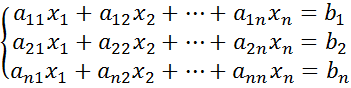 ∆=
∆=
Правило Крамера для любой системы линейных уравнений
1.∆≠0 то система (*) имеет 1решение,которое находится по формулам:
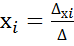 i=1,2,3,4…
i=1,2,3,4…
2.∆=0, а хотя бы один из вспомогательных определителей 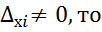 система (*) не имеет решений.
система (*) не имеет решений.
3.∆=0  , то система (*) имеет бесконечное число решений.
, то система (*) имеет бесконечное число решений.
n-мерным вектором х наз. Упорядоченный набор действительных чисел (коордиат) х=( )
)
Векторы равны если равны их соотв. Координаты.
Для n-мерных векторов справедливо:
1.Сложение(складываются соотв координаты)
2.Умножение на действительное число(*каждая координата)
3Сколярное произведение (х,у)=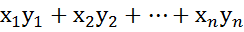
4.Длина вектора.│х│=