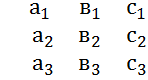Определители

1.Определителем 2порядка называется число, опр по формуле ∆==

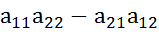
2.Определителем 3порядка наз. Число, опр по формуле ∆=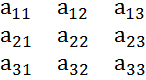

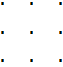= правило Сарруса (правило треуг.)

3.Определителем n-ого порядка наз ∆ определяемый с помощью табл.∆=(**)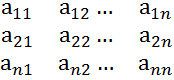

3.Свойства определителей.

Транспонирование – определитель (**) наз. Такое его преобразование, при кот. Его строки становятся столбцами с теми же самыми номерами.

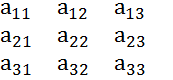
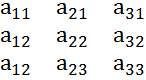Св-во1.Определитель не меняется при транспонировании

Пример1.∆= ∆=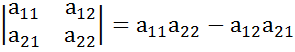

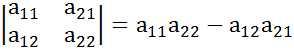
Св-во2.Если какая-нибудь строка определителя состоит из одних нулей, то его значение=0

Св-во3.При перестановке местами любых 2х строк определитель меняет знак.

Пример.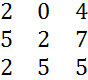=20+100-16-7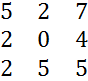0=34 =16+70-20-100=-34 =16+70-20-100=-34

Св-во4.Определитель, сод. 2одинаковые строки = 0 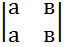=ав-ав=0

Св-во5.Общий множитель всех элементов строки можно выносить за знак определителя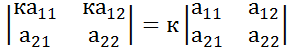

Св-во7.Если все элементы i-й строки определителя n-ого порядка представлены в виде суммы 2х слагаемых 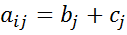=1,2,3…n ,то определитель равен сумме 2х определителей у которых все строки кроме такие же как в заданном определителе, а i–я трока в одном из слагаемых состоит из 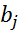,а в другом из элементов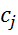

=+

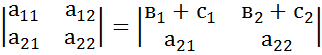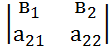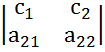
Св-во8.Если одна из строк определителя есть линейная комбинация его других строк, то определитель = 0 (следствие из св-ва7, св-ва6)

Св-во9.Определитель не меняется если к элементам одной из его строк +/- соответственные элементы др строки умноженные на одно и то же число.

=+=
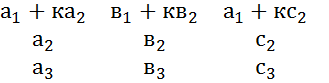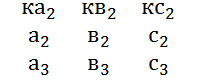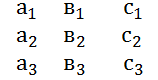