Сравнительная оценка особенности непрерывных и цифровых систем

Повышение точности в установленном режиме

Методы оценки качества регулирования

Оценка качества регулирования линейных систем

 

1.Методы оценки качества регулирования.

При исследовании САУ приходится решать задачу обеспечения требуемых показателей качества переходного процесса:

- быстродействия,

- колебательности,

- перерегулирования,

характеризующих точность и плавность протекания процесса.

Будем считать, что САУ описывается системой дифференциальных уравнений с постоянными коэффициентами.

 

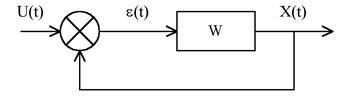
При изменении воздействия U(t) на входе выходную величину можно записать так:

 

x(t) = x_св(t) + x_в(t),

 

где: x(t) – решение дифференциального уравнения, описывающего САУ,

x_св(t) – свободная составляющая переходного процесса (соответствующая общему решению однородного дифференциального уравнения),

x_в(t) – вынужденная состовляющая переходного процесса, обусловленная законом изменения U(t) и определяющая точность САУ.

 

1. Оценка качества регулирования в установившемся режиме.

Установившаяся ошибка регулирования САУ e_в(t) = U(t) – x_в(t), которую можно представить в виде ряда:

,

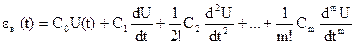где C₀ … C_m - коэффициенты ошибок, при этом:

С₀ = W(0) - коэфф. статической и позиционной ошибки;

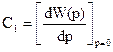- коэффициент скоростной ошибки;

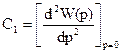
коэфф. ошибки от ускорения;

W - передаточная функция замкнутой САУ.

 

В статических системах С₀ ¹ 0, в САУ с астатизмом 1-го порядка С₀ = 0 , С₁ ¹ 0, в САУ с астатизмом 2-го порядка С₀ = C₁ = 0, С₂ ¹ 0. Увеличение числа интегрирующих звеньев повышает порядок астатизма, что ведет к уменьшению ошибки, но при этом усложняется обеспечение устойчивости системы.

 

2. Оценка качества переходного процесса при воздействии ступенчатой функции.

Пусть U(t) = 1(t) , тогда по кривой переходнойхарактеристикиможно получить прямые оценки качества переходного процесса:

1) время регулирования t_р –минимальное время по истечении которого регулируемая величина будет оставать­ся близкой к устанавливаемомузначению с,заданной точностью D = | h(t) – h_уст |,значение D нужно оговаривать в процентах oт h_уст;

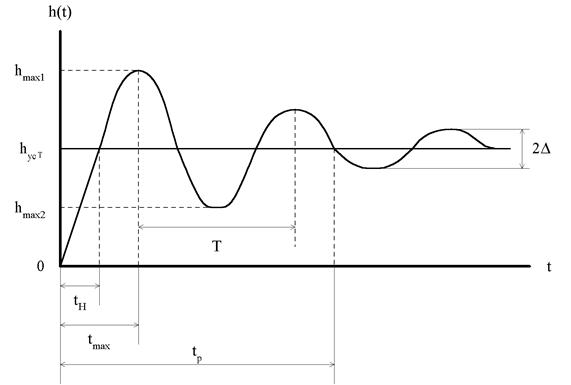
2) перерегулирование s - максимальное отклонение h(t) от h_уст в относительных единицах или процентах от h_уст;

3) Частота колебаний w=2p/T;

4) Число колебаний n, которое имеет переходная характеристика за время t_р чаще всего n =1¸2 иногда 3¸4;

5) время достижения первого максимума t_max;

6) время нарастания переходного процесса t_н;

7) декремент затухания:

.

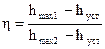Переходные процессы делят на три группы:

- монотонные (a);

- апериодические (b);

- колебательные (c).

 

1. Оценка качества регулирования при гармонических воздействиях, ощуществляющихся по АЧХ.

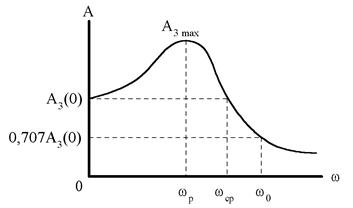
А₃ - АЧХ замкнутой САУ.

Для оценки качества переходного процесса используются следующие характеристики.

1) 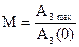- показатель колебательности. Чем выше М, тем менее качественна САУ. Считается допустимым 1,1<M<1,5;

2) w_р - резонансная частота СДУ;

3) полоса пропускания САУ - это интервал 0<w<w₀;

4) частота среза w_ср - косвенно характеризует длительность переходного процесса.

.

2.Повышение точности в установившемся режиме. Проблема обеспечения требуемых свойств линейных систем требует решения следующих задач:

- обеспечение устойчивости (стабилизация);

- повышение запаса устойчивости (демпфирование);

- повышение точности регулирования в установившемся режиме (уменьшение или устранение статической ошибки воспроизведения задающего воздействия, уменьшение или устранение влияния возмущающих воздействий);

- улучшение переходных процессов (увеличение быстродействия, максимальное уменьшение динамических ошибок воспроизведения, воздействия).

Если для анализа цифровых систем используется Z - преоб­разование или уравнение состояния в дискретной форме, то их реакции представляются только в моменты квантования. Поэтому к дискретным данным нужно подходить осторожно, т.к. они могут быть неточным представлением истинной реакции цифровой системы. Из рисунка, на котором изображен типичный выходной сигнал цифровой системы С(t), имеющий максимальное значение С_m и соответствующий ему дискретный сигнал C^*(t) видно, что максимальное значение дискретного сигнала:

.

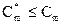Чем меньше T, тем меньше различие между 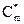и С_m. Но если Т велик, то дискретное представление реакции может быть совер­шенно ошибочным. Отметим, что выбор Т обычно определяется не правильностью представления её реакции в моменты квантования, а что более важно, соображениями устойчивости, точности и качества системы в целом.

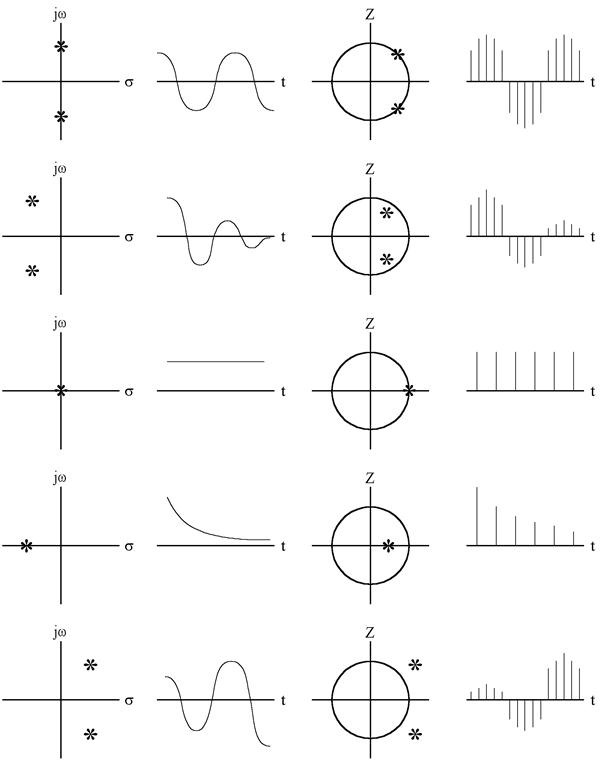
Для непрерывных систем известна связь между положением на S - плоскости корней характеристического уравнения и пере­ходной функцией. Например, комплексно-сопряженные корни, распо­ложенные в левой половине S - плоскости, обуславливают экспонен­циально затухающие синусоидальные процессы, корни на отрица­тельной части действительной оси соответствуют монотонно за­тухающим процессам; простые сопряженные корни на мнимой оси приводят к возникновению незатухающих гармонических колеба­ний с постоянной амплитудой. Кратные корни на мнимой оси и корни в правой половине S - плоскости соответствуют расходящимся процессам.

 

3.Сравним характерные особенности непрерывных и цифровых систем, используя в качестве примера систему управления кос­мическим кораблем. Структурная схема упрощенной системы управ­ления по одной координате изображена на рисунке.

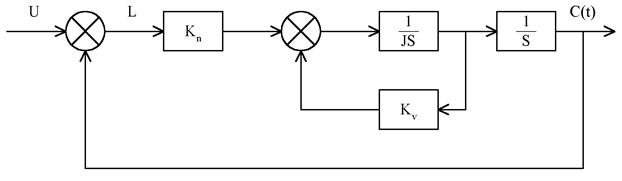
K_n, K_v –датчики положения и скорости.

Предполагается, что корабль имеет жесткую структуру. Поэтому его можно представить чистым моментом инерции J. По поло­жению c(t) и его производной - скорости V(t) - с помощью соответствующих датчиков осуществляется обратная связь. Обрат­ная связь по скорости часто используется для целей стабилиза­ции.

Передаточная функция разомкнутой системы:

.

Передаточная функция замкнутой системы:

.

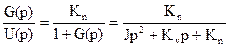Для реального корабля:

K_n = 1,65 × 10⁶, K_v = 3,17 × 10⁵, J = 41822.

Тогда

.

Характеристическое уравнение системы:

p² + 8,871p + 39,453 = 0.

Корни уравнения положительны при любых положительных K_n, K_v, J, следовательно, непрерывная система будет асимптотически устойчива.

Структурная схема соответствующей цифровой системы отличается от предыдущей наличием квантователя нулевого порядка с периодом T.

 

Передаточная функция разомкнутой системы:

,

 

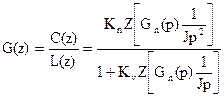где G_n(p) - переходная функция экстраполятора, известно, что:

.

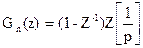Тогда:

,

.

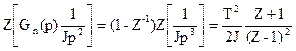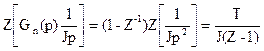Тогда:

.

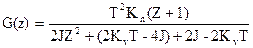Передаточная функция замкнутой системы:

.

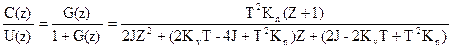При K_n = 1,65 × 10⁶, K_v = 3,17 × 10⁵, J = 41822,

,

где A = 83644,

B = 1,65 × 10⁶ × T² + 6,34 × 10⁵ × T – 167288,

C = 1,65 × 10⁶ × T² - 6,34 × 10⁵ × T + 83644.

Качество цифровой системы зависит от параметров K_n, K_v, J и Т. Если применить критерий Джури к характеристическому уравнению системы Az² + Bz + C = 0, то диапазон устойчивости по параметру Т будет равен:

0 £ Т < 264 с

Корневой годограф, т.е. диаграмма положения корней характериестического уравнения на плоскости Z при изменении Т от нуля до бесконечности, представлен на рисунке:

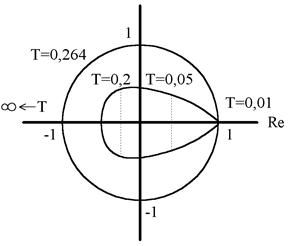
Переходные функции цифровой системы изображены на рисунке:

 

Из рассмотренного примера, по результатам анализа непрерывной и цифровой систем управления, можно сделать выводы:

1) При одних и тех же структуре и параметрах цифровая система менее устойчивая, чем непрерывная.

2) Качество цифровой системы зависит от периода квантования. Его возрастание обычно способствует увеличению выброса переходной функции и, в конечном счете, может привести к неустойчивости системы.

3) При малых значениях Т корни характеристического уравнения располагаются очень близко к точке Z = 1. Это создает практические сложности при анализе цифровых систем, т.к. некоторые параметры (кривые коэффициенты затухания, перерегулирования и. др.) определяются не точно.