Примеры.
Число: –1. Число: –127
Код модуля числа: 00000001 Код модуля числа: 01111111
Обратный код числа: 11111110 Обратный код числа : 10000000
Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
Дополнительный код числа –1: Дополнительный код числа –127:


Используя прямой, обратный и дополнительный коды, можно свести операцию умножения к последовательности сложений и сдвигов, а операцию деления – к многократному прибавлению к делителю дополнительного кода делителя.
Отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа [31].
3.5. Вещественные числа
Вещественные числа (конечные и бесконечные десятичные дроби) хранятся и обрабатываются в компьютере в формате с плавающей запятой.
Формат чисел с плавающей запятой базируется на экспоненциальной форме записи, в которой может быть представлено любое число. Так, число А может быть представлено в виде
A = m× qn,
где т – мантисса числа; q – основание системы счисления; п –порядок числа.
Для однозначности представления чисел с плавающей запятой используется нормализованная форма, при которой мантисса отвечает условию
1/n = ½m½ < 1.
Это означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля.
Пример.Преобразуем числа в экспоненциальную форму с нормализованной мантиссой:
421,637 = 0,421637 ´ 103; 0,000286 = 0,286 ´ 10-4.
Число в форме с плавающей запятой занимает в памяти компьютера 4 или 8 (зависит от точности) байт. При записи числа с плавающей запятой выделяют разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Арифметические операции.При сложении и вычитании чисел в формате с плавающей запятой сначала производится подготовительная операция выравнивания порядков. Порядок меньшего
(по модулю) числа увеличивается до величины порядка большего (по модулю) числа. Для того чтобы величина числа не изменилась, мантисса уменьшается в такое же число раз (сдвигается в ячейке памяти вправо на число разрядов, равное разности порядков чисел).
После выполнения операции выравнивания одинаковые разряды чисел оказываются расположенными в одних и тех же разрядах ячеек памяти. Теперь операции сложения и вычитания чисел сводятся к сложению или вычитанию мантисс.
После выполнения арифметической операции для приведения полученного числа к стандартному формату с плавающей запятой производится нормализация, т.е. мантисса сдвигается влево или вправо так, чтобы ее первая значащая цифра попала в первый разряд после запятой [14].
Пример.Произвести сложение чисел 0,1 × 23 и 0,1 × 25 в формате с плавающей запятой.
Произведем выравнивание порядков и сложение мантисс:
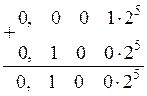
При умножении чисел в формате с плавающей запятой порядки складываются, а мантиссы перемножаются. При делении из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя.
Пример.Произвести умножение чисел 0,1 ´ 23 и 0,1 ´ 25 в формате с плавающей запятой. После умножения будет получено число 0,01 ´ 28, которое после нормализации примет вид 0,1 ´ 27.
 |
Лекция 4
Логические основы компьютера
4.1. Логические выражения и логические операции
Логика – наука о законах и формах мышления. К основным понятиям логики относятся нижеперечисленные.
Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно. Например, высказывание «сегодня хорошая погода» является истинным, если светит солнце, нет ветра и дождя и т.д. В противном случае это же высказывание будет ложным.
Утверждение – суждение, которое требуется доказать или опровергнуть, например, сумма внутренних углов треугольника равна 180°.
Рассуждение– цепочка высказываний или утверждений, определенным образом связанных друг с другом, например, если хотите начать работать на компьютере, то необходимо сначала включить электропитание.
Умозаключение– логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение.
Область знаний, которая изучает истинность или ложность высказываний (суждений), называется математической логикой. Утверждения в математической логике называются логическими выражениями.
Для обработки логических выражений в математической логике была создана алгебра высказываний, или алгебра логики. Основы такой алгебры были заложены в трудах английского математика Джорджа Буля (XIX в.), булева алгебра.
Решение любой задачи на компьютере сводится к выполнению процессором ряда арифметических и логических операций. Они выполняются над логическими выражениями на основе законов и правил булевой алгебры.
Логическая операция конъюнкция
Конъюнкциейназывается логическая операция, ставящая в соответствие двум простым логическим выражениям новое сложное логическое выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных (простых) логических выражения.
Конъюнкция определяет соединение двух логических выражений (высказываний) с помощью союза И. Эта операция называется также логическим умножением и обозначается символами & или ^.
Рассмотрим таблицу истинности.
| A | B | A&B |
Логическая операция дизъюнкция
Дизъюнкция определяет логическое соединение двух логических выражений (высказываний) с помощью союза ИЛИ.
Эта операция называется также еще логическим сложением и обозначается значком v. Рассмотрим таблицу истинности.
| A | B | AÚB |
В соответствии с таблицей истинности можно дать определение.
Дизъюнкцией называется логическая операция, ставящая в соответствие двум простым логическим выражениям новое сложное логическое выражение, которое будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) логических выражений.
Логическая операция отрицание (инверсия)
Определяется над одним аргументом (простым или сложным логическим выражением) следующим образом: если исходное выражение истинно, то результат его отрицания будет ложным, и наоборот, если исходное выражение ложно, то его отрицание будет истинным.
Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Операция отрицание обозначается символом ┐(¬), а ее результат определяется следующей таблицей истинности:
| A | ┐A |
Логическая операция импликация (логическое следование)
Эта операция связывает два простых логических выражения, из которых первое является условием, а второе – следствием из этого условия. В разговорном языке эта операция выражается словами если..., то... .
Для ее обозначения в алгебре логики используется значок следования =>. Результат операции импликации для условия А (первое логическое выражение) и условия В (второе логическое выражение) определяется в соответствии со следующей таблицей истинности:
| A | B | A B B
|
По определению результатом импликации является ЛОЖЬ тогда и только тогда, когда условие (А) истинно, а следствие (В) ложно.
Логическая операция эквивалентность
(равнозначность)
Данная операция определяет результат сравнения двух простых логических выражений А и В, обозначается символом <=>. Результат этой операции – новое логическое выражение, которое является истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны.
Таблица истинности:
| A | B | A B B
|
Сложным логическим выражением называется логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью рассмотренных логических операций [26].
Пусть, например, А, В и С – три простых логических выражения. Одним из примеров составленного из них сложного логического выражения будет
D =  Ù (BÚC).
Ù (BÚC).
Порядок выполнения логических операций в сложном логическом выражении:
1) инверсия – 1;
2) конъюнкция – & (или л);
3) дизъюнкция – Ú;
4) импликация – =>;
5) эквивалентность – <=>.
Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Построим таблицу истинности для заданного сложного логического выражения:
| A | B | C | 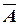
| BÚC | 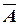 Ù(BÚC) Ù(BÚC)
|
4.2. Логические законы и правила преобразования
логических выражений
В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений.
Закон тождества. Всякое высказывание тождественно самому себе:
A = A.
Закон непротиворечия.Высказывание не может быть одновременно истинным и ложным. Если высказывание Л истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно:
А &  = 0.
= 0.
Закон исключенного третьего.Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение «истина»:
А Ú = 1.
= 1.
Закон двойного отрицания.Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание:
 = А.
= А.
Законы де Моргана:
 &
&
 Ú
Ú .
.
Закон коммутативности.В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:
| Логическое умножение | Логическое сложение |
| А&В = В&А | АÚВ = АÚВ |
Закон ассоциативности.Если в логическом выражении используется только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять:
| Логическое умножение | Логическое сложение |
| (А&В)&С = А&(В&С) | (АÚВ)ÚС = АÚ(ВÚС) |
Закон дистрибутивности. В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые [14]:
| Дистрибутивность умножения относительно сложения | Дистрибутивность сложения относительно умножения |
| ab + ac = a(b + c) – в алгебре (A&B)Ú(A&C) = A&(BÚC) | (АÚВ)&(AÚC) = АÚ(В&C) |
Рассмотрим в качестве примера применения законов логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение:
(A&B)Ú(A& ).
).
Воспользуемся законом дистрибутивности и вынесем за скобки А:
(A&B)Ú(A& ) = A&(BÚ
) = A&(BÚ ).
).
По закону исключенного третьего В Ú В = 1, следовательно:
A&(BÚ ) = A&1 = A.
) = A&1 = A.
4.3. Базовые логические элементы
Базовые логические элементы реализуют рассмотренные три основные логические операции:
– логический элемент «И» – логическое умножение;
– логический элемент «ИЛИ» – логическое сложение;
– логический элемент «НЕ» – инверсию.
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Логический элемент «И».На входы А и В логического элемента (рис. 1) подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения.
 |

Логический элемент «ИЛИ».На входы А и В логического элемента (рис. 2) подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.

Логический элемент «НЕ».На вход А логического элемента (рис. 3) подается сигнал 0 или 1. На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии.

4.4. Сумматор двоичных чисел
В целях максимального упрощения работы компьютера все многообразие математических операций в процессоре сводится к сложению двоичных чисел. Поэтому главной частью процессора являются сумматоры, которые как раз и обеспечивают такое сложение.
Полусумматор.При сложении двоичных чисел в каждом разряде образуется сумма, и при этом возможен перенос в старший разряд. Введем обозначения слагаемых (А, В),переноса (Р)и суммы (S).
| Слагаемые | Перенос | Сумма | |
| А | В | P | S |
Из таблицы видно, что перенос можно реализовать с помощью операции логического умножения:
P = A&B.
Значения суммы близки к результату операции логического сложения (кроме случая, когда на входы подаются две единицы, а на выходе должен получиться нуль).
Нужный результат достигается, если результат логического сложения умножить на инвертированный перенос. Таким образом, для определения суммы можно применить следующее логическое выражение:
S = (AÚB)&( ).
).
Построим таблицу истинности для данного логического выражения и убедимся в правильности нашего предположения (табл. 5).
Таблица 5