Фундаментальные принципы управления

Модели объектов управления

Анализ объекта управления

Понятия системы управления

Фундаментальные принципы управления

Методы оценки качества регулирования линейных систем

Оптимизация настройки систем управления

Законы управления и параметры настроек цифровых регуляторов

Устойчивость линейных систем

Сведения из теории Z-преобразования

Линейные системы с постоянными параметрами

Техника и теория цифрового управления (обзор)

Понятия адаптивного управления

Понятия оптимального управления

Основные виды автоматического управления

Элементарные звенья и структурные схемы систем управления

Применение преобразования Лапласа

Уравнения линейных систем управления

Фундаментальные принципы управления

Содержание

Пермь, 2009 г.

Конспекты лекций

по дисциплине “Основы теории управления”

 

Курс лекций по дисциплине “Основы теории управления”, читаемый в течении 5-го семестра студентам специальностей 2201, 2202, отвечает требованиям Государственного образовательного стандарта. Основная цель этого курса состоит в изучении и освоении студентами фундаментальных понятий теории автоматического управления, относящихся к линейным системам. Курс состоит из 14-ти разделов, в каждом из которых в самом начале изложения учебного материала приводится список подразделов. Наименование этих подразделов соответствует контрольным вопросам на зачете по данному курсу.

Рекомендуемая литература.

 

Основная. 1. Основы теории автоматического управления. Под ред. А.А. Воронова, часть 1, М.: Высш. Шк., 1986.

Дополнительная. 2. Фельдбаум А.А. Бутковский А.Г. Методы теории автоматического управления, Наука, М.:, 1971.

3. Александров А.Г. Оптимальные и адаптивные системы. М.: Высш. Шк., 1989.

4. Острём К., Виттенмарк Б. Системы управления с ЭВМ, Мир, М.:, 1987.

 

1.Предметом изучения теории управления является система управления. Прежде чем дать понятие системы управления рассмотрим отдельно понятие системы и понятие управления.

Общепринятого понятия системы не существует. Мы будем использовать определение системы, данное фон- Берталанфи, австрийским ученым-биологом.

Система – это множество элементов произвольной материальной природы, находящихся в некоторых заданных отношениях друг к другу.

 

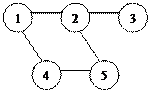Структуру системы удобно изображать в виде графа, вершинами которого являются элементы 1, 2, 3, 4, 5, а дуги соответствуют отношениям между элементами. Например, дуга 4-5, отображает отношение между элементами 4 и 5.

Количество элементов в системе ограничено числом 10¹⁰⁰. Оно соответствует бесконечности. Например, число атомов во всей вселенной равно примерно 10⁷³.

Число отношений между элементами может быть существенно больше числа 10¹⁰⁰. Американский ученый У.Эшби приводит в качестве примера табло, состоящее из двадцати рядов электрических лампочек по двадцать лампочек в ряду. Число состояний (отношений) этого табло равно 2⁴⁰⁰»10¹²⁰, что гораздо больше числа 10¹⁰⁰.

 

Система обладает свойствами, наиболее важными из которых являются:

1) наблюдаемость (измеримость),

2) управляемость,

3) устойчивость.

Наблюдаемость – это свойство, которое позволяет оценивать характеристики (параметры) системы. Измеримость связана с наблюдаемостью, и это свойство позволяет получать информацию о параметрах системы с помощью технических устройств, измерительных приборов или датчиков.

Свойство управляемости связано с возможностью перевода системы из точки А в точку В.

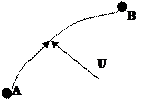Если с помощью воздействий U можно перевести систему из А в В, то система управляема, если не удастся, то тогда она не управляема.

В теории автоматического управления рассмотрено порядка 20 видов управляемости системы. Один из видов – это перевод из любой точки 3D в любую другую точку 3D.

Процесс формирования воздействий, которые переводят систему из одного состояния в другое, называется управлением. Более того, само воздействие U называется управлением.

Устойчивость – это свойство, позволяющее системе находиться в заданном равновесном состоянии при воздействии на нее возмущений. Устойчивость и управляемость противоречивы.

Немного о терминологии. Понятие управление имеет ряд синонимов, каждый из которых отличается от других своей спецификой. Наиболее общее понятие об управлении несет в себе термин “кибернетика”. Первым его употребил, по-видимому, греческий ученый и философ Платон (4 в. до н.э.), как искусство управления кораблем. Французкий ученый А. Ампер (1834г.) предложил назвать кибернетикой науку об управлении человеческим обществом. Современное определение кибернетики дал американский ученый Н.Винер (1948г.), который назвал кибернетикой науку об управлении и связи в живом организме и машине. Более узкое понятие “управление” (русск.), “control” (английск.) относится к управлению в технических системах и имеет наиболее широкое распространение в технической литературе.

Ещё более узкое понятие “регулирование” характерно для особого класса систем и рассматривается как управление по отклонению.

Теперь дадим определение системы управления.

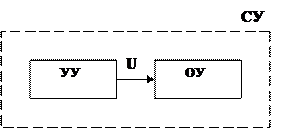Система управления (СУ) – это совокупность обьекта управления и устройства управления (УУ), которое вырабатывает управляющие воздействия U, переводящее в заданное состояние.

 

 

 

 

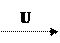
2.В теории автоматического управления (ТАУ) решается два вида задач: задачи анализа (разложения) ОУ и задачи синтеза (соединения, создания) УУ. Анализ или исследование ОУ производится на языке ТАУ, в соответствии с которым многомерный объект описывается с помощью векторов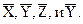

 

 

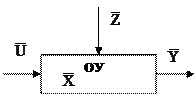X=(x₁, x₂,…, x_n) – вектор состояния,

U=(u₁, u₂,…, u_m) – вектор управления,

Z=(z₁, z₂,…, z_p) – вектор влияния окружающей среды, (вектор помех),

Y=(y₁, y₂,…, y_q) – вектор регулируемых переменных.

Анализ объекта управлений – получение информации о состовляющих векторах X, Y, Z, U.

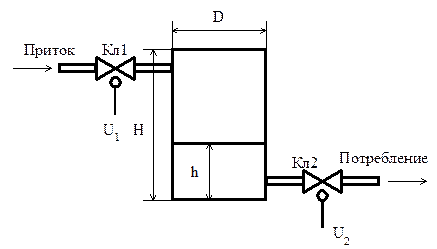
Пример1. Объектом управления является емкость, хранящая жидкий продукт, который поступает в емкость через клапан Кл1.

Потребление продукта осуществляется через клапан Кл2.

Вектор состояния =(x₁, x₂, x₃, x₄, x₅, x₆), где

x₁ – высота Н, x₂ – диаметр D, x₃ – объем жидкости,

x₄ – уровень h, x₅ – величина притока, x₆ – величина потребления.

Вектор влияния окружающей среды 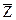=(z₁, z₂), где

z₁ – температура окружающей среды,

z₂ – атмосферное давление.

Вектор регулируемых переменных =(y₁), где y₁ – уровень h.

 

 

Вектор управления 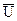=(u₁, u₂), где u₁ – управление по притоку, u₂ – управление по потреблению.

Целью анализа ОУ является сбор информации для создания математической модели ОУ.

 

3.Математическая модель ОУ есть некоторое соотношение (в виде математического выражения), которое устанавливает связь между воздействиями (входами) на ОУ и его реакцией (выходами). Воздействия – это составляющие векторов 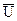и 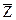, реакции - это составляющие векторов и. В общем виде математическая модель представляется выражением:

=A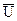, где А – обобщенный оператор, который и называется математической моделью. В данном случае А – это матрица, но для одномерного ОУ это может быть число, или функция. Для примера1 математическими моделями будут:

1) x₅= k₁u₁, где k₁ – пропускная способность клапана Кл1.

2) x₆= k₂u₂, где k₂ – пропускная способность клапана Кл2.

3) x₃= (k₁u₁- k₂u₂)t , t – время,

4) =

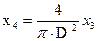Если модель устанавливает связь между входом и выходом ОУ с достаточной точностью, то такая модель называется адекватной. На практике можно использовать только адекватные модели.

Существует два подхода определения математической модели:

1) дедуктивный (аналитический), для простых объектов управления математическая модель выводится на основании физических законов, как для примера 1.