Точность замкнутых импульсных систем

Рис. 1.16

Заметим, что наибольшее влияние на рост АЧХ разомкнутой системы оказывает увеличение коэффициента усиления, а ФЧХ изменяется только при изменении постоянных времени разомкнутой системы.

Таким образом, косвенными показателями качества импульсной системы, определяемыми по годографу разомкнутой импульсной системы являются:

1. Запас устойчивости по амплитуде DА^*=1-

где ; .

2. Запас устойчивости по фазе , где - частота среза, при которой , т.е. амплитудно-частотная характеристика разомкнутой импульсной системы равна единице.

С определенными выше показателями качества связано понятие предельного коэффициента усиления системы K_пр– такого коэффициента усиления разомкнутой импульсной системы, при котором запас устойчивости по амплитуде становится равным нулю, т.е. замкнутая импульсная система находится на границе устойчивости.

Значение К_пр.можно найти из очевидной пропорции:

K ® A_p

K_пр _®1, откуда K_пр=.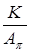

Напомним, что коэффициент усиления импульсной системы с передаточной функцией и n=0 определяется как ,

а при nV1 как .

По логарифмическим частотным характеристикам разомкнутой импульсной системы

Как изложено в разделе ____ , построение логарифмических частотных характеристик разомкнутой импульсной систем с дискретной передаточной функцией производится после ее преобразования к соответствующей непрерывной с помощью билинейного преобразования, т.е заменой z=, или .,

где - получило название относительной, а l=w -- абсолютной псевдочастоты [3].

Заметим, что билинейное преобразование является приближенным, погрешность этого преобразования мала при малых значения

(при этом граничным значением является частота ), поэтому l и носит название псевдочастоты..

После вышеприведенного преобразования строятся логарифмические аиплитудно-частотные (ЛАЧХ) и фазо-частотные (ЛФЧХ) характеристики, по тем же правилам, что и соответствующие логарифмические характеристики непрерывных разомкнутых систем..

По построенным логарифмическим характеристикам можно судить об устойчивости замкнутой импульсной системы и определять запасы устойчивости по амплитуде и фазе (рис.1.17).

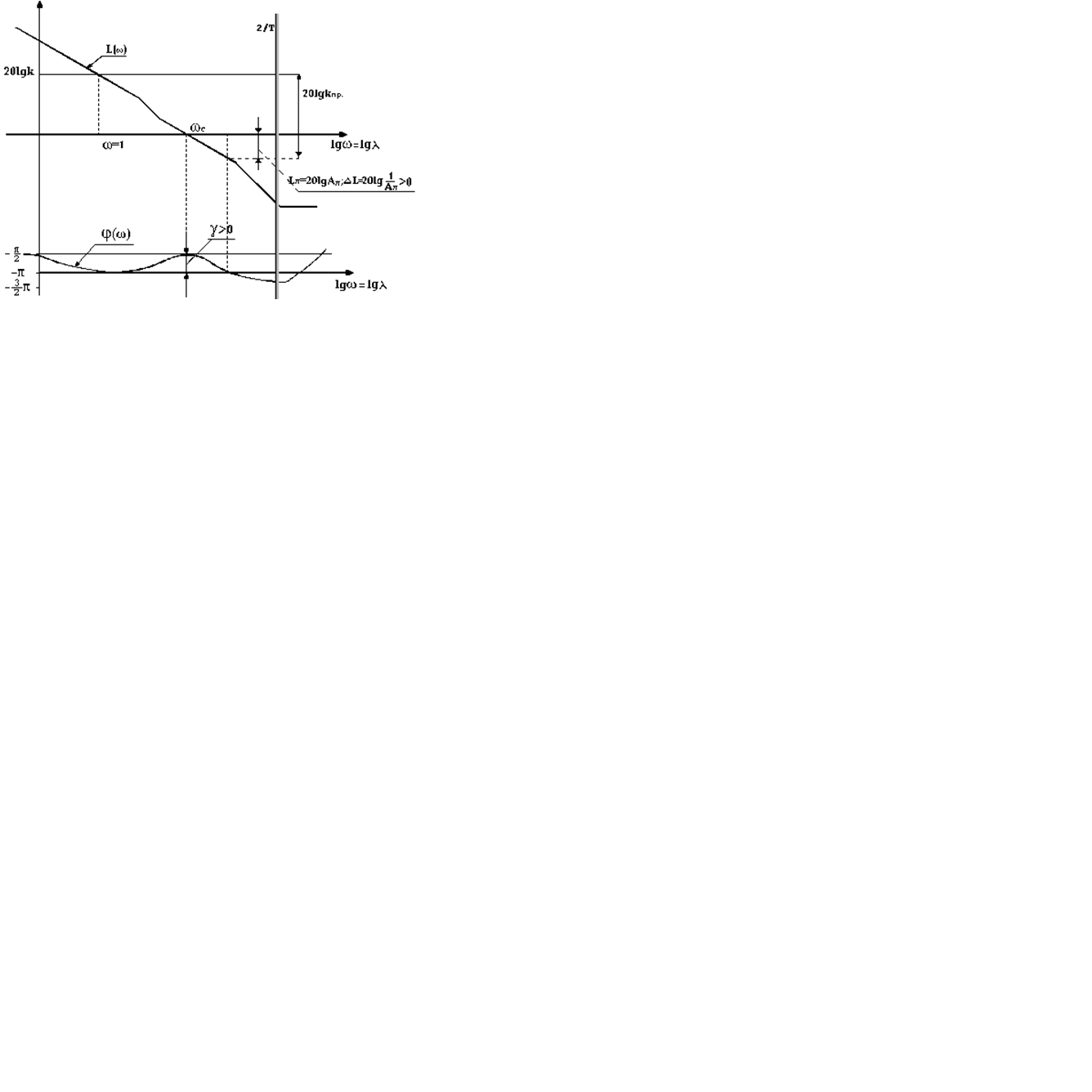
Рис.1.17

Таким образом, косвенными показателями качества импульсной системы, определяемыми по логарифмическим частотным характеристикам разомкнутой импульсной системы являются:

1. 1. Логарифмический запас устойчивости по амплитуде

DL=0-L_p=L(1)-L_p=20 lg;

где ; .

Корневые методы анализа качества импульсных систем

Корневые методы анализа качества применительно к непрерывным системам, в основном, сводятся к решению двух задач :

· · определению области расположения корней характеристического уравнения исследуемой системы ;

· · оценке переходных процессов по найденным параметрам области расположения корней.

Следует отметить, что построение переходных процессов для замкнутых импульсных систем по имеющейся дискретной передаточной функции производится намного проще, чем для непрерывных и сводится к расчету по рекуррентным формулам (см._____ ).

Поэтому в этом разделе мы рассмотрим только одну задачу – определение минимальной удаленности корня характеристического полинома исследуемой системы от мнимой оси, называемой степенью устойчивостии характеризующей быстродействие системы. Малая степень устойчивости определяется большой постоянной времени системы и характеризует малое быстродействие системы. И, наоборот, большая степень устойчивости характеризует системы с большим быстродействием.

По аналогии с непрерывными системами степень устойчивости () импульсных систем можно определить из условия нахождения так называемой смещенной дискретной передаточной функции на границе устойчивости.

Для решения этой задачи можно воспользоваться любым критерием устойчивости импульсных систем, и в частности критерием Гурвица.

Системы с конечной длительностью переходного процесса

В общем случае, процессы в устойчивой импульсной системе протекают неограниченно долго. Однако, в отличие от непрерывных систем, возможны такие условия, при которых процесс длится конечное время.

Это возможно в том случае, когда весовая, или импульсная переходная функция импульсной системы заканчивается за некоторое конечное число тактов Т. Для дискретной передаточной функции

;

процессы описываются разностным уравнением:

Очевидно, что переходной процесс в системе завершится за (n-1) тактов, если , т.е. дискретная передаточная функция замкнутой импульсной системы имеем вид :

;

Ординаты весовой, или импульсной переходной функции такой системы равны , m=0,1,2….,n-1.

Определим степень устойчивости системы с конечной длительностью переходного процесса , для чего запишем выражение для смещенной дискретной передаточной функции:

Из характеристического уравнения следует, что смещенная система будет устойчива при любом значении l₀, в том числе при l₀=. Это значит, что

Система с конечной длительностью процесса обладает бесконечной степенью устойчивости.

Точность замкнутых импульсных систем, так же как и непрерывных, определяется ошибкой, возникающей в системе при отработке степенных входных сигналов, описываемых функциями вида 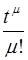. Рассмотрим точность системы так называемой типовой структуры, представленной на рис. 1.

Рис.1

К такому виду с помощью структурных преобразований можно привести большинство замкнутых импульсных систем.

Рассмотрим ошибки, возникающие в такой системе при отработке управляющего сигнала x _y (t).

Предположим, что непрерывная передаточная функция разомкнутой системы

где к – коэффициент усиления разомкнутой системы,

n - разность между числом интегрирующих и дифференцирующих звеньев в разомкнутой системе , называемая порядком, или степенью астатизма системы по управлению Заметим, что порядок астатизма равен разности числа множителей типа в знаменателе и числителе дискретной передаточной функции ..

Ошибку замкнутой импульсной системы при отработке управляющего воздействия можно найти по формуле

где, как известно из раздела ____;

- дискретные изображения управляющего сигнала, регулируемого и сигнала ошибки по управлению соответственно;

- дискретные передаточные функции разомкнутой системы и замкнутой системы ошибки по управляющему сигналу.

Дискретная передаточная функция разомкнутой системы , имеющая n интегрирующих звеньев будет иметь вид

Дискретное изображение степенного входного сигнала порядка m имеет вид

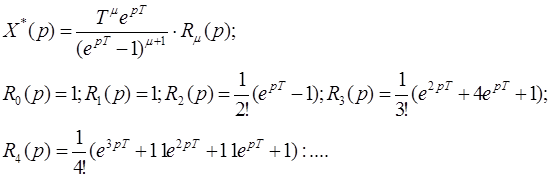
Выражение для произвольного m приведено в [2]. Заметим, что Rm(0)=1 для всех m.

Таким образом, ошибка замкнутой системы по управляющему воздействию может быть найдена из выражения:

Следует отметить, что найденное выражение совпадает с аналогичными выражениями ошибок по управлению в замкнутой непрерывной системе .

Рассмотрим ошибки, возникающие в такой системе при отработке возмущающего сигнала x В (t).

Для определения передаточной функции ошибки системы по управлению запишем уравнения в операторном виде, описывающие элементы системы (рис.1).

Воздействуя на правую и левую часть равенства оператором -преобразования, получим

откуда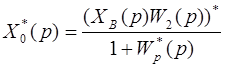

Таким образом, ошибку замкнутой импульсной системы по возмущающему воздействию следует искать по формуле

Следует отметить, что выражение означает, что сначала надо перемножить непрерывные изображения, а затем от произведения переходить к дискретному изображению по Лапласу.

Приведем окончательную формулу ошибки во возмущающему воздействию, аналогичную выведенной ранее для ошибки по управлению.

где n - порядок (степень) астатизма системы по возмущению, равный разности числа интегрирующих и дифференцирующих звеньев в передаточной функции , т.е. лежащих до точки приложения возмущающего воздействия , или множителей типа в знаменателе и числителе дискретной передаточной функции .

Пример

Найдем ошибки в системе, представленной на рис.2.

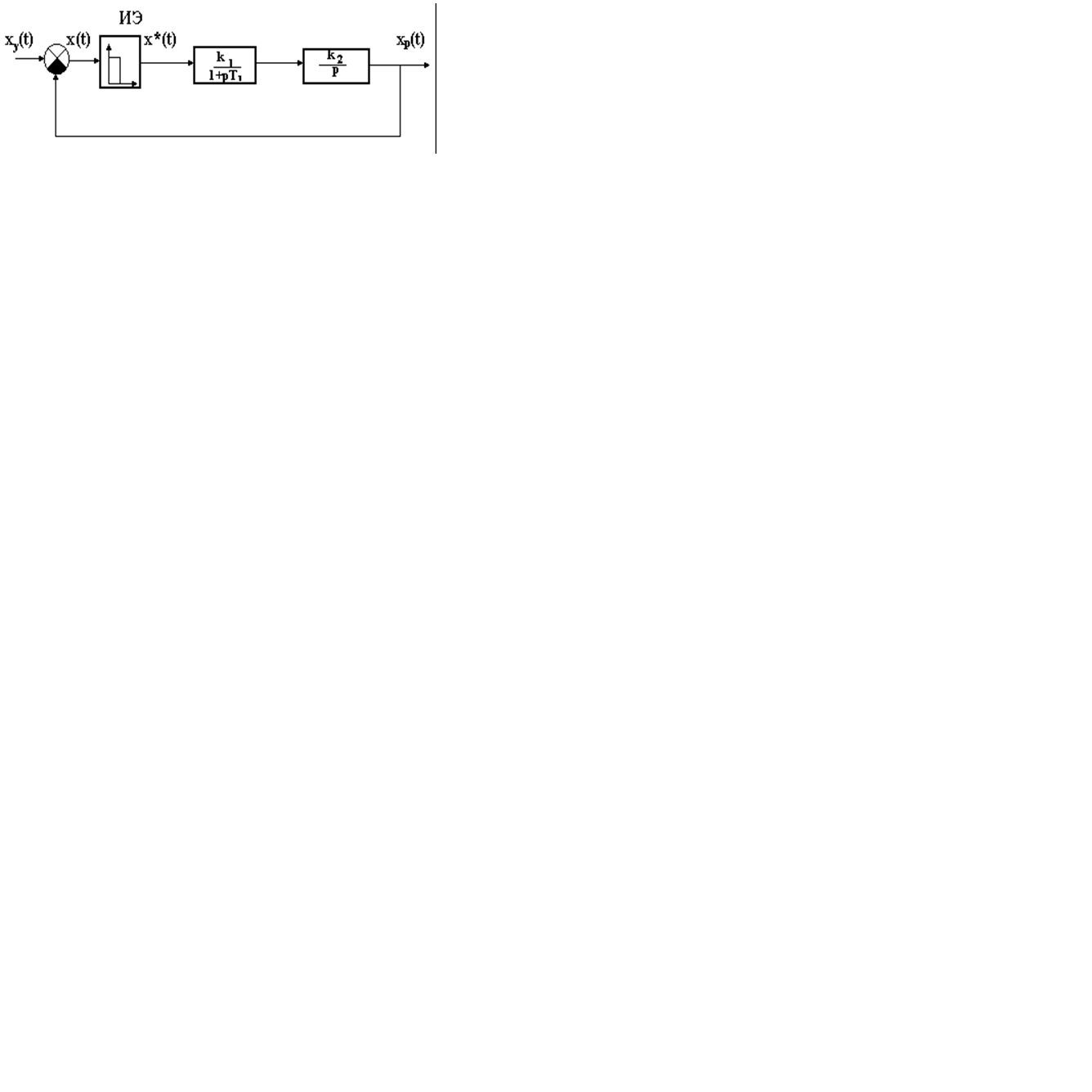
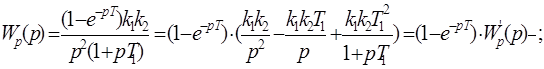
Найдем дискретное преобразование Лапласа от выражения , приведенного в круглых скобках

Умножив полученное выражение на , получим выражение дискретной передаточной функции разомкнутой системы в виде

Поскольку порядок астатизма системы по управлению известен и равен n=1 (числу интегрирующих звеньев), то сразу можно ответить на вопрос о величине статической ошибки по управлению, возникающей в замкнутой импульсной системе при отработке ступенчатого воздействия.

Поскольку в этом случае m<n, то ошибка в соответствии с выведенной формулой будет нулевой, то есть в системе с астатизмом первого порядка ступенчатый входной сигнал отрабатывается с нулевой ошибкой.

Рассчитаем кинетическую ошибку по управлению в замкнутой импульсной системе, для чего приведем выражение для к дробно-рациональному виду

Кинетическую ошибку по управлению можно найти по формуле

Таким образом система отрабатывает линейно возрастающий управляющий сигнал с конечной ошибкой, прямо пропорциональной уровню входного сигнала, обратно пропорциональной коэффициенту усиления разомкнутой системы

Найдем ошибку по возмущению. Порядок астатизма системы по возмущению равен n=0, так как звено не содержит интегрирующих звеньев. Таким образом имеет смысл говорить о статической ошибке, поскольку система с астатизмом нулевого порядка отрабатывает единичное ступенчатое воздействие с конечной ошибкой, а линейно возрастающее – с бесконечной ошибкой.

Найдем выражение для Из выражения

Следует, что ,

Откуда

Таким образом система отрабатывает ступенчатый возмущающий сигнал с конечной ошибкой, прямо пропорциональной уровню входного сигнала и обратно пропорциональной коэффициенту усиления разомкнутой системы звеньев, лежащих до точки приложения возмущения.

56 . Нелинейные САУ . Типовые Н . Э .

Естественные Н. Э. -ограничены « энергетически ». , гистерезис , плохое исполнение .

Искусственные Н. Э. - вводятся искусственно в систему , чтобы обеспечить качественно новые процессы в системе .

Далее рассматриваются нелинейные системы , состоящие из нелинейного статического элемента и линейной динамической системы .

57 . Структурные схемы нелинейных САУ . Некоторые правила их преобразования .

Линия передачи -1

Узел -2

Линейное динамическое звено -3

Нелинейный статический элемент -4

Три вида описания Н . Э .

1) 1) графический

2) 2) аналитический f(x)=arctg(x)

3) 3) кусочно-линейная аппроксимация

B ; x>=a

f(x)= - B ; x<=a

0 ; модуль(х)<a

Соединение нелинейных статических элементов .

Особенности Н . САУ .

Принцип суперпозиции не выполняется

y=y1+y2 , для линейных систем (принцип выполняется ) ; y<>y1+y2 для нелинейных САУ .

1) 1) в линейной части системы можно производить любые структурные преобразования .

2) 2) нельзя переставлять Н . Э . между собой

3) 3) нельзя переставлять линейные и Н . Э .

4) 4) нелинейные статические элементы можно переносить через узел ветвления .

При переносе статического нелинейного элемента через узел по (против) направления передачи сигнала в отходящую от узла ветвь следует добавить нелинейный элемент с прямой (обратной ) характеристикой.

58 . Основные понятия фазовой плоскости , свойства фазовых траекторий . Примеры .

Исследование динамики Н . С . на фазовой плоскости .

n ^го порядка .

; -начальные условия .

-вектор (решение системы ) , -вектор состояния системы .

при изменении t вектор описывает траекторию в n -мерном пространстве , называемым фазовым. Для n<=2 используют графический метод (метод фазовой плоскости ) .

n=2 (плоскость ) .

x₂=f(x₁)-изображающая точка , значение уравнения в точке .

При разных начальных значениях получается совокупность фазовых траекторий (фазовый портрет ) .

Свойства фазовых траекторий :

1) 1) При однозначных f₁(x₁,x₂) и f₂(x₁,x₂) - однозначная , для каждой точки x_{1 ,} x₂определено однозначно . Фазовые траектории не пересекаются , за исключением точек , называемых особыми .

2) 2) Фазовые траектории заканчиваются в точках , соответствующих положениям равновесия .

, (нет движения ) . особые точки .

Нелинейная система второго порядка использует в качестве первой координаты сигнал отклонения (ошибки ) , а второй координаты - производную ,, .

3) 3) Движение изображающий точки происходит слева направо (в верхней полуплоскости ) , а в нижней - справа налево . Изображающая точка движется по часовой стрелке .

4) 4) Пересечение фазовыми траекториями оси абсцисс происходит под прямым углом .

, , на оси абсцисс х принимает максимальные и минимальные значения .