Основные понятия и принципы анализа переходных процессов

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Если к цепи приложено постоянное напряжение U, то в цепи протекает постоянный ток I=U/R, а если к цепи приложено синусоидальное напряжение и=U_msinωt, то в цепи с постоянными параметрами протекает синусоидальный ток i=I_msin(ωt-φ).

Такие токи устанавливаются лишь через некоторое время после включения цепи или после изменения ее параметров и могут существовать все время, пока к ней приложено напряжение и параметры остаются неизменными. Эти токи называются установившимися токами, а соответствующие напряжения на отдельных участках цепи – установившимися напряжениями.

Каждому установившемуся режиму электрической цепи соответствует строго определенное энергетическое состояние, т. е. определенные значения энергии электрического поля конденсатора и магнитного поля индуктивной катушки:

,

Любое изменение состояния электрической цепи (включение, отключение, изменение параметров цепи и т. п.) называется коммутацией. Будем считать, что процесс коммутации осуществляется мгновенно. Энергетическое же состояние цепи не может измениться мгновенно.

Пусть, например, в цепи при разомкнутом выключателе В протекает установившийся ток , определяемый только сопротивлением R цепи. При замыкании выключателя, т. е. при шунтировании резистора R₁ установившийся ток в цепи .

Если предположить, что ток в цепи изменяется мгновенно от I₁ до I₂, то это будет означать, что в индуктивной катушке в этот момент времени переменным током индуцируется ЭДС самоиндукции

Но любая ЭДС самоиндукции препятствует изменению тока в цепи. Поэтому предположение о мгновенном изменении тока в цепи неверно. Только в идеальном случае, когда L=0, можно рассматривать изменение тока как мгновенное.

Таким образом, ток в цепи с индуктивностью не может измениться скачком. В этом заключается первый закон коммутации.

Согласно второму закону коммутации, напряжение на зажимах конденсатора или другого емкостного элемента не может измениться скачком.

Индуктивные и емкостные элементы являются инерционными, вследствие чего для изменения энергетического состояния электрической цепи требуется некоторый промежуток времени, в течение которого происходит переходный процесс. Длительность переходного процесса зависит от параметров цепи. Хотя такой процесс обычно длится несколько секунд или даже доли секунды, токи и напряжения в это время на отдельных участках цепи могут достигать больших значений, иногда опасных для электроустановок. Поэтому нужно уметь рассчитывать токи и напряжения переходных процессов и на основании этих расчетов разрабатывать меры защиты электрической цепи.

Как любой динамический процесс в материальных системах, так и переходный процесс в электрических цепях описывается дифференциальным уравнением. Режим линейных электрических цепей с постоянными параметрами R, L и С описывается линейным дифференциальным уравнением с постоянными коэффициентами. Так, режим цепи синусоидального тока при последовательном соединении R, L и С и напряжении источника питания описывается уравнением

Полное решение такого неоднородного линейного дифференциального уравнения с постоянными коэффициентами ищут в виде

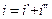
где i’ – частное решение данного неоднородного уравнения; i" – общее решение однородного дифференциального уравнения.

Ток i' поддерживается в цепи напряжением источника питания и является установившимся током. Ток i" находят при решении уравнения без свободного члена. Физически это означает, что приложенное к цепи напряжение равно нулю, т. е. цепь представляет замкнутый контур, состоящий из последовательно соединенных R, L и С. Ток в такой цепи может поддерживаться только за счет запасов энергии в магнитном поле индуктивной катушки или в электрическом поле конденсатора. Так как эти запасы ограничены и при протекании тока i" по элементам с сопротивлением R происходит рассеяние энергии в виде теплоты, то через некоторое время этот ток становится равным нулю.

Ток i" называется свободным, так как его определяют в свободном режиме цепи.

Таким образом, полное решение дифференциального уравнения позволяет определить ток i в цепи в переходном режиме или напряжение на элементах цепи .