Общая формулировка критерия Найквиста

Рис.1.12

Заметим, что годограф охватывает точку с координатами (0,0) один раз в положительном направлении (против часовой стрелки), аналогично годограф охватывает точку с координатами (-1,j0) в положительном направлении один раз .

Сформулируем критерий устойчивости Найквиста для случая б).

Если разомкнутая импульсная система неустойчива и ее характеристический полином имеет L корней, лежащих вне окружности единичного радиуса, то для устойчивости замкнутой импульсной системы необходимо и достаточно, чтобы амплитудно-частотная характеристика разомкнутой системы охватывала точку с координатами (-1, j0) в положительном направлении (против часовой стрелки) L раз при изменении частоты в диапазоне 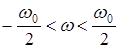и L/2 раз при изменении частоты в диапазоне.

Таким образом, замкнутая импульсная система (рис.1.12 б) устойчива, если характеристический полином разомкнутой импульсной системы имеет 2 корня вне единичной окружности.

c) c) Разомкнутая импульсная система нейтральна и ее характеристический полином имеет n нулевых корней, т.е. ее дискретная передаточная функция и комплексный коэффициент усиления имеют вид:

.

Амплитудно-фазовая характеристика при малых w начинается в бесконечности. Если рассматривать как предел некоторой функции устойчивой разомкнутой импульсной системы, т.е.

то можно показать, подобно тому, как это было сделано для непрерывных систем, что годографы и отличаются друг от друга дугой бесконечно большого радиуса длиной np./2, проведенной к действительной оси и называемой «дополнением в бесконечности» (рис.1.13).

 

 

 

 

 

 

 

 

Рис.1.13

 

Сформулируем критерий устойчивости Найквиста для случая в).

Если разомкнутая импульсная система нейтральна и ее характеристический полином имеет n нулевых корней, то для устойчивости замкнутой импульсной системы необходимо и достаточно , чтобы амплитудно-фазовая характеристика разомкнутой импульсной системы вместе с «дополнением в бесконечности» не охватывала точку с координатами (-1,j0).

 

Все три формулировки критерия устойчивости Найквиста для замкнутых импульсных систем можно объединить, приведя общую формулировку, подобно аналогичной формулировке для непрерывных замкнутых систем.

Замкнутая импульсная система устойчива, если алгебраическая сумма переходов годографом разомкнутой импульсной системы вместе с «дополнением в бесконечности» отрезка действительной оси (-, -1) равна L при изменении частоты в диапазоне 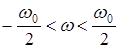или L/2 при изменении частоты в диапазоне, где L – число корней Z i характеристического полинома A^*(z) , лежащих вне окружности единичного радиуса.

На рис.1.14 представлены переходы отрезка действительной оси

(-, -1) с соответствующими весами.