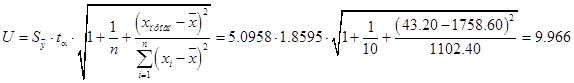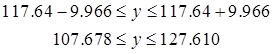Найдем параметры уравнения линейной регрессии и дадим экономическую интерпретацию коэффициента регрессии.

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию ГОУ ВПО

Всероссийский заочный финансово-экономический институт

Кафедра финансового менеджмента

 

Контрольная работа

по дисциплине «Эконометрика»

вариант № 4

 

 

Выполнила:

 

№ зачетной книжки

 

Принял:

 

Пенза 2010

Задача.

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (Y, млн. руб.).

Таблица 1.

Зависимость объема выпуска продукции от объема капиталовложений.

X
Y

Требуется:

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α = 0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F - критерия Фишера (α = 0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α = 0,1, если прогнозное значения фактора Х составит 80% от его максимального значения.

7. Представить графически фактические и модельные значения Y точки прогноза.

8. Составить уравнения нелинейной регрессии и построить их графики:

· гиперболической;

· степенной;

· показательной.

9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Найдем параметры уравнения линейной регрессии и дадим экономическую интерпретацию коэффициента регрессии.

Уравнение линейной регрессии имеет вид: ,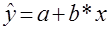

где

Вычисления для нахождения параметров a и b приведены в таблице 2.

Таблица 2.

Расчет значений для нахождения параметров уравнения линейной регрессии.

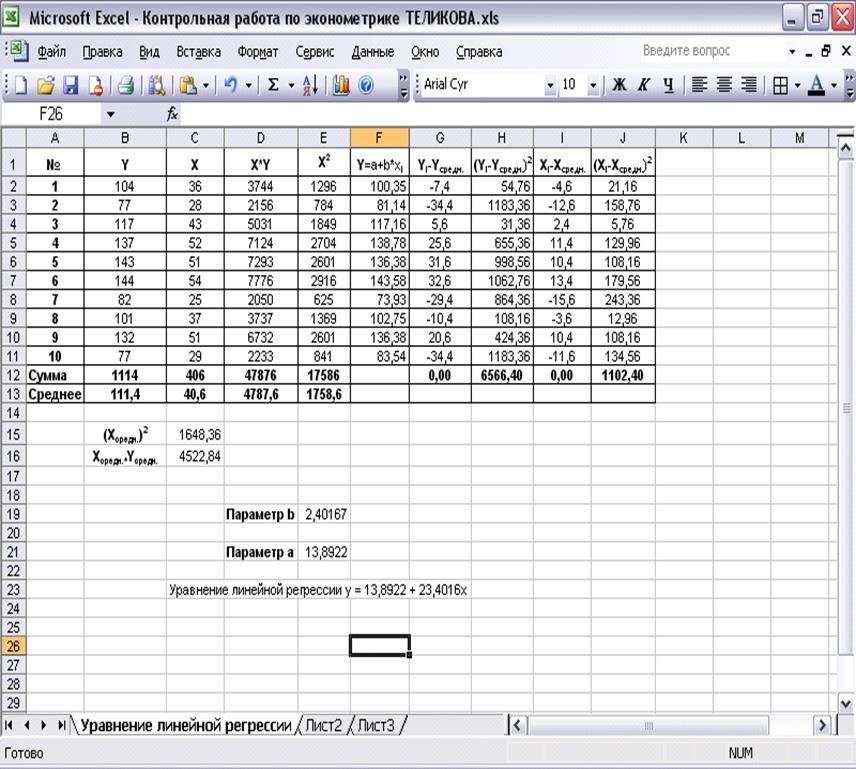
Уравнение регрессии имеет вид: y = 13,8951 + 2,4016*x.

С увеличением объема капиталовложений (X) на 1 млн. руб. объем выпускаемой продукции (Y) увеличится в среднем на 2,4016 млн. руб. Таким образом, наблюдается положительная корреляция признаков, что свидетельствует об эффективности работы предприятий и выгодности капиталовложений в их деятельность.

2. Вычислим остатки; найдем остаточную сумму квадратов; оценим дисперсию остатков и построим график остатков.

Остатки вычисляются по формуле: e_i = y_i – y _прогн.

Остаточная сумма квадратов отклонений: = 207,74.

Дисперсия остатков: 25.97.

Расчеты приведены в таблице 3.

Таблица 3.

№	Y	X	Y=a+b*xi	ei = yi - yпрогн.	ei2
			100,35	3,65	13,306
			81,14	-4,14	17,131
			117,16	-0,16	0,0269
			138,78	-1,78	3,1649
			136,38	6,62	43,859
			143,58	0,42	0,1744
			73,93	8,07	65,061
			102,75	-1,75	3,0765
			136,38	-4,38	19,161
			83,54	-6,54	42,78
Сумма				0,00	207,74
Среднее	111,4	40,6

График остатков имеет вид:

Рис.1. График остатков

3. Проверим выполнение предпосылок МНК, который включает элементы:

-проверка равенства математического ожидания случайной составляющей нулю;

-случайный характер остатков;

-проверка независимости;

-соответствие ряда остатков нормальному закону распределения.

Проверка равенства математического ожидания уровней ряда остатков нулю.

Осуществляется в ходе проверки соответствующей нулевой гипотезы H_0: . С этой целью строится t-статистика 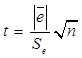, где _.

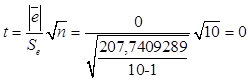
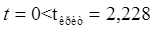, таким образом, гипотеза принимается.

Случайный характер остатков.

Проверим случайность уровней ряда остатков с помощью критерия поворотных точек:

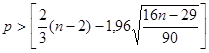
Количество поворотных точек определяем по таблице остатков:

№	ei = yi - yпрогн.	Точки поворота	ei2	(ei - ei -1)2
	3,65		13,31
	-4,14	*	17,13	60,63
	-0,16	*	0,03	15,80
	-1,78	*	3,16	2,61
	6,62	*	43,86	70,59
	0,42	*	0,17	38,50
	8,07	*	65,06	58,50
	-1,75	*	3,08	96,43
	-4,38		19,16	6,88
	-6,54		42,78	4,68
Сумма	0,00		207,74	354,62
Среднее

= 6 > [4,3029], следовательно, свойство случайности остатков выполняется.

Независимость остатков проверяется с помощью критерия Дарбина – Уотсона:

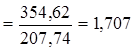
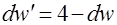=4 – 1,707 = 2,293.

Так как 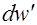попало в интервал от d₂ до 2, то по данному критерию можно сделать вывод о выполнении свойства независимости. Это означает, что в ряде динамики не имеется автокорреляции, следовательно, модель по этому критерию адекватна.

Соответствие ряда остатков нормальному закону распределения определяется с помощью R/S-критерия с критическими уровнями (2,7-3,7);

Рассчитаем значение RS:

RS = (e_max - e_min)/ S,

где e_max - максимальное значение уровней ряда остатков E(t) = 8,07;

e_min - минимальное значение уровней ряда остатков E(t) = -6,54.

S - среднеквадратическое отклонение, 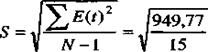= 4,8044.

RS = (e_max - e_min)/ S= (8,07+6,54)/4,8044 = 3,04.

Так как 2,7<3,04<3,7, и полученное значение RS попало в за­данный интервал, значит, выполняется свойство нормальности распределения.

Таким образом, рассмотрев различные критерии выполнения предпосылок МНК, приходим к выводу, что предпосылки МНК выполняются.

4. Осуществим проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента α = 0,05.

Проверка значимости отдельных коэффициентов регрессии связана с определением расчетных значений t-критерия (t–статистики) для соответствующих коэффициентов регрессии:

 

 

 

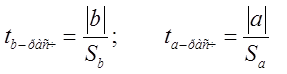
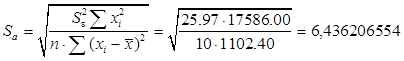
Затем расчетные значения сравниваются с табличными t_табл=2,3060. Табличное значение критерия определяется при (n-2) степенях свободы (n - число наблюдений) и соответствующем уровне значимости a (0,05)

Если расчетное значение t-критерия с (n-2) степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, коэффициент регрессии считается значимым.

В нашем случае коэффициенты регрессии a₀- незначимый, а₁- значимый коэффициенты.

 

 

5. Вычислим коэффициент детерминации, проверим значимость уравнения регрессии с помощью - критерия Фишера 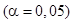, найдем среднюю относительную ошибку аппроксимации. Сделаем вывод о качестве модели.

Определим линейный коэффициент парной корреляции по формуле

 

Рассчитаем коэффициент детерминации:

0,968

Он показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов.

Чем ближе R² к 1, тем лучше качество модели.

Вариация результата Y (объема выпуска продукции) на 96,8 % объясняется вариацией фактора X (объемом капиталов­ложений).

Оценку значимости уравнения регрессии проведем с помо­щью F-критерия Фишера:

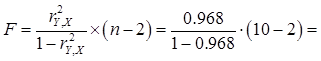244,869

 

F>F_табл.=5.32 для α=0,05; k₁=m=1; k₂=n-m-1=8

 

Уравнение регрессии с вероятностью 0,95 в целом статис­тически значимое, т. к. F > Fтабл.

Определим среднюю относительную ошибку аппроксимации:

 

3,863%

В среднем расчетные значения у для линейной модели от­личаются от фактических значений на 3,863%

Так как ошибка аппроксимации данной модели меньше 7%, то это свидетельствует о хорошем качестве модели.

6. Осуществим прогнозирование среднего значения показателя при уровне значимости , если прогнозное значения фактора Хсоставит 80% от его максимального значения.

Прогнозное значение показателя, если прогнозное значение фактора X составит 80% от его максимального значения 0,8*54,00=43,20, составит:

y _прогн =13,89+2,40*43,20=117,64.

Интервальный прогноз:

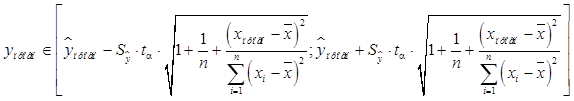
для 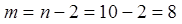степеней свободы и уровня значимости 0,1 равно 1,8595.

Тогда