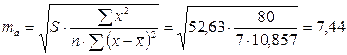Анализ точности определения оценок коэффициентов регрессии

В силу случайного отбора элементов в выборку случайными являются также оценки а и b истинных коэффициентов регрессии и теоретического уравнения регрессии. При этом оценки тем надежнее, чем меньше их разброс вокруг и , то есть чем меньше дисперсия D(a) и D(b) оценок. Надежность получаемых оценок тесно связана с дисперсией случайных отклонений . Фактически является дисперсией переменной Y относительно линии регрессии .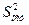

Корень квадратный из необъясненной дисперсии называется стандартной ошибкой оценки (стандартной ошибкой). .

и называются стандартными ошибками коэффициентов регрессии.

 

Они определяются по формулам:

Объяснение данных соотношений имеет наглядную графическую интерпретацию. Коэффициент b определяет наклон прямой регрессии. Чем больше разброс Y вокруг линии регрессии, тем больше ошибка определения наклона прямой регрессии.

Дисперсия свободного члена уравнения регрессии пропорциональна . Действительно, чем сильнее меняется наклон прямой, тем больше разброс значений свободного члена, характеризующего точку пересечения этой прямой с осью Oy.

Для нашего примера величина стандартной ошибки коэффициентов регрессии составила:

.