Моменты системы двух СВ.

Начальным моментом порядка k,s системы (X,Y) называется математическое ожидание произведения X^kY^s

Центральным моментом порядка k,s системы (X,Y) называется математическое ожидание произведения отклонений

где

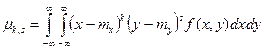
Дисперсии:

Дисперсия характеризует рассеивание случайной точки в направлении осей Ox и Oy.

Особую роль как характеристика системы играет смешанный центральный момент порядка 1,1, называемый ковариацией:

Также ковариацию называют корреляционным моментом и моментом связи. Он характеризует связь между величинами X и Y. Можно доказать, что для независимых СВ ковариация равна нулю. Таким образом, если ковариация отлична от нуля, это есть признак наличия зависимости между X и Y.

Помимо связи, ковариация характеризует еще и рассеивания величин X и Y. Если одна из величин (X,Y) мало отклоняется от своего математического ожидания (почти не случайна), то ковариация будет мала, какой бы тесной ни была связь. Поэтому для того, чтобы охарактеризовать только связь в чистом виде, переходят от к безразмерной величине

Эта характеристика называет коэффициентом корреляции величин X и Y. Как и для ковариации, коэффициент корреляции для независимых СВ равен нулю. СВ, для которых коэффициент корреляции равен нулю, называются некоррелированными (несвязанными).

Если коэффициент корреляции близок или равен нулю, то это не всегда означает, что величины X и Y независимы. Например, если плотность распределения (X, Y) выражена как

то, например, если X=0, Y может принимать

значения от -r до r, а если X=r, то Y=1. То есть

вообще говоря, Y зависит от X. Но если рассчитать

коэффициент корреляции, то получим, что r_xy=0.

Коэффициент корреляции характеризует не всякую зависимость, а только линейную. Линейная зависимость заключается в том, что при возрастании одной СВ другая имеет тенденция возрастать, либо убывать по линейному закону . Такая линейная зависимость может быть более или менее ярко выражена, а может даже приближаться к функциональной. В случае, если выполняется

то (+ для a>0, - для a<0). Во всех других случаях

Для положительных r говорят о положительной корреляции, а для r<0 – об отрицательной. Положительная корреляция говорит о том, что с возрастанием одной величины другая имеет тенденцию возрастать. Отрицательная корреляция говорит о том, что с возрастанием одной величины другая имеет тенденцию убывать.

Примеры:

1. Вес (X) и рост (Y) человека связаны положительной корреляцией.

2. Время, потраченное на подготовку к экзамену (X) и оценка (Y).

Если в нашем распоряжении имеются результаты опытов над системой двух СВ (выборки), то о наличии связи можно судить по графику.

На первом рисунке положение точек говорит о наличии явно выраженной положительной корреляции. Еще большая корреляция (r практически =1 – функциональная зависимость) наблюдается на рис.2. На третьем рисунке можно наблюдать слабую отрицательную корреляцию. Всегда перед проведением исследования следует построить график!

Свойства коэффициента корреляции:

1. r_xx=0

2. r_xy= r_yx

3.

4. Если СВ X и Y независимы, то r_xy=0

5. тогда и только тогда, когда y=a+bx