Статическая САР напряжения генератора

 

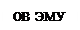
Рис. I. 14. Принципиальная электрическая схема

статической САР напряжения генератора.

 

Здесь обозначено

Г – генератор, якорь которого вращается от постороннего двигателя с постоянной угловой скоростью w = const;

ОВГ – обмотка возбуждения генератора;

ЭМУ – электромашинный усилитель, предназначенный для усиления сигнала по току;

ОВ ЭМУ – обмотка возбуждения электромашинного усилителя;

ЭУ – электронный усилитель для усилений сигнала по напряжению;

Rн – сопротивление нагрузки генератора;

Iэму, Iг, I - токи, соответственно, в обмотках возбуждения ЭМУ, Г и нагрузке;

П – потенциометр задания.

Здесь объектом управления ОУ является генератор со своей ОВ Г, все остальные элементы схемы составляют регулирующее устройство РУ.

Цель САР – обеспечить поддержание постоянства напряжения генератора при изменении его нагрузки. Величину напряжения Uг, которую генератор должен поддерживать с некоторой точностью на своих зажимах, несмотря на колебания Rн, задается с помощью напряжения Uзд, снимаемого с потенциометра П.

Непосредственно из рис. I.14 можно получить зависимости, которые понадобятся нам в дальнейшем:

UГ = Е г– I × R я , (I.5.1)

и

DU = Uзд – Uг . (I.5.2),

где Е г– ЭДС генератора,

R я – сопротивление якорной цепи.

Из принципиальной схемы САР напряжения генератора получим функциональную схему. Начинать построение функциональной схемы рекомендуется с сумматора, который в принципиальной схеме представлен частью электрической схемы, предназначенной для сравнения сигналов Uзд и Uг. Полученный в соответствии с формулой (I.5.2) сигнал рассогласования DU поступает далее по цепочке – ЭУ, ЭМУ, Г. Выходной сигнал генератора по цепи отрицательной обратной связи поступает на сумматор. Отметим также, что на генератор воздействует возмущение R н.

Рис. I. 15. Функциональная схема статической САР генератора напряжения.

 

В установившемся режиме напряжение генератора Uг, а, следовательно, и Iг , и Iэму постоянны.

Пусть в некоторый момент времени нагрузка на генератор скачкообразно изменится (допустим, ток нагрузки I скачком возрастает). Из (I.5.1) видно, что в этом случае Uг в первый момент скачком уменьшится, а напряжение рассогласования DU согласно (I.5.2) скачком возрастает. Этот сигнал DU после усиления будет в процессе регулирования восстанавливать упавшее в первый момент напряжение Uг. До какого значения будет подниматься этот сигнал Uг? Будет ли он равен после окончания переходного процесса напряжению Uзд? В статической САР – никогда. Действительно, в случае равенства Uг и Uзд согласно (I.5.2) DU будет равно нулю, а это означает, что и IЭМУ, и Ir и, самое главное, Uг должны быть равны нулю, что противоречит назначению САР – поддерживать с некоторой точностью постоянным напряжение на зажимах генератора.

Таким образом, наличие в установившемся режиме статической ошибки DU ¹ 0 является необходимым для функционирования системы. Именно эта ошибка DU после ее усиления электронным и электромашинным усилителям и определяет величину Uг. Нетрудно понять, что величина этой статической ошибки обратно пропорциональна коэффициенту усиления прямой цепи (см. рис. I.15), ибо, чем больше этот коэффициент усиления, тем меньше должна быть ошибка DU, чтобы получить требуемое Uг. Перейдем теперь к математической стороне дела.

Рассмотрим сначала отдельно взятый генератор без регулирующего устройства. Мы уже знаем, что напряжение на зажимах генератора определяется выражением (I.5.1). Из этого выражения следует, что при холостом ходе, когда R н® ¥ , т.е. I = 0, имеет место равенство

Uгхх= Е г.

При номинальной нагрузке I = Iн

 

Uгн = Е г – I нR я.

Следовательно, изменение напряжения на генератора в установивше6мся режиме от изменения нагрузки от I = 0 и I = Iномбез регулирующего устройства DUг без ру (т.е. статическая ошибка, соответствующая указанному изменению нагрузки) будет

DUг без ру = Uгхх – Uгн = Е г – Ег + I нR н = I нR я . (I.5.3)

 

Теперь обратимся к рис. I.15, т.е. случаю, когда помимо объекта управления – генератора – присутствует и регулирующее устройство.

Будем считать, что рабочая точка находится на линейных участках характеристик элементов САР, поэтому

где Еэму– ЭДС ЭМУ.

Подставив в это уравнение для Ег значения Еэмуи Iэму, получим

.

С учетом полученного выражения для Ег соотношение (I.5.1) примет вид

.

Обозначив

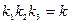
и принимая во внимание (I.5.2), получим

или

.

Тогда

. (I.5.4)

Видно, что выходная (регулируемая) величина Uг линейно зависит от тока нагрузки I. Найдем изменение напряжения на генераторе с регулирующим устройством при изменении нагрузки от I = Iхх= 0 до I = Iн . При холостом ходе, т.е. при Iхх= 0 из (I.5.4) следует, что

.

При достаточно большом коэффициенте усиления k, величину которого можно легко менять за счет изменения коэффициента усиления kэ электронного усилителя, соотношение близко к единице, и, следовательно, (здесь статической ошибки, определяемой величиной IR я, нет).

При номинальной нагрузке

появляется статическая ошибка

. (I.5.5)

Из сравнения (I.5.3) и (I.5.5) ясно, что в САР напряжения генератора по сравнению с одиночным генератором (без регулирующего устройства) статическая ошибка уменьшается в (1 + k) раз. Рассмотрим статические характеристики САР генератора при наличии и отсутствии регулирующего устройства (рис. I.16).

Для удобства примем при холостом ходе , тогда статические характеристики САР при наличии и отсутствии регулирующего устройства начнутся при I = Iхх= 0 из одной точки.

Рис. I. 16. Статические характеристики САР при

наличии и отсутствии регулирующего устройства.

Видно, что для различных значений нагрузки появляется различная по величине статическая ошибка (она растет с ростом тока нагрузки I), причем для САР с регулирующим устройством статическая ошибка значительно меньше, чем без регулирующего устройства. Из (I.5.5) ясно, что для уменьшения статической ошибки надо увеличивать коэффициент усиления системы k, имея, правда, в виду (это будет показано в дальнейшем), что с ростом k уменьшается устойчивость системы.

Мы рассмотрели статическое управление при изменении нагрузки. Аналогично можно рассмотреть статическое уравнение при изменении задающего сигнала.