И выявление его структуры

Ранее отмечался тот факт, что величина каждого последующего уровня временного ряда в значительной мере зависит от величины его предыдущего уровня. Интенсивность такой взаимозависимости, т. е. теснота статистической связи между двумя элементами временного ряда, измеряется парным коэффициентом корреляции. Заметим, что вычисление коэффициента корреляции проводят между величинами, принадлежащими одному и тому же ряду, поэтому его принято называть коэффициентомавтокорреляции.

Таким образом, автокорреляция уровней ряда – это корреляционная связь между уровнями одного и того же ряда динамики, сдвинутыми на определенный промежуток времени L. Натуральное число L называется лагом и представляет собой расстояние между членами временного ряда, для которых оценивается корреляционная связь. Например, автокорреляция порядка L – это взаимосвязь двух последовательностей y_t = (y₁, y₂, ..., y_n_-_L ) и y_t₊_L = (y₁₊_L, y₂₊_L, y_n ).

Интенсивность (теснота) линейной связи для указанных последовательностей оценивается с помощью уже известной нам формулы (2), в которой 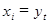, , 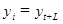а величина n заменяется на n – L:

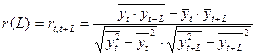. (23)

Отметим, что коэффициенты автокорреляции r(L) являются безразмерными величинами, а значения r(L) могут изменяться в пределах от –1 до +1. Очевидно, что r(0) = 1, так как это коэффициент корреляции члена ряда с самим собой.

Отметим также, что r(L) в (23) вычисляются по выборочным данным, т. е. являются случайными величинами. Поэтому оценки r(L) обязательно сопровождаются проверкой на существенность их отличия от нуля. С этой целью наблюдаемое значение статистики Стьюдента

сравнивают с критическим значением t(α/2;n). Здесь α – заданный уровень значимости, а число степеней свободы ν определяется в зависимости от числа уровней ряда, включенных в формулу (23). При проверке линейной связи .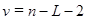

Если | t | > t(α/2;n) – то коэффициент автокорреляции существенный (статистически значим). Напротив, при | t | < < t(α/2;n) линейная связь между членами временного ряда, отстоящими друг от друга на лаг L, отсутствует.

С увеличением лага L уменьшается число пар значений, по которым рассчитывается коэффициент автокорреляции. Считается, что для обеспечения статистической достоверности коэффициентов r(L) максимальный лаг не должен превышать величину n/4, где n – число наблюдений (уровней ряда).

Последовательность коэффициентов автокорреляции первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда r(L), график r(L)называют коррелограммой.

Практическое значение автокорреляционной функции состоит в том, что она характеризует структуру временного ряда, а именно:

- если наиболее высоким оказался коэффициент автокорреляции первого порядка r(1), то изучаемый ряд содержит линейную тенденцию;

- если наиболее высоким оказался коэффициент автокорреляции порядка L, то изучаемый ряд содержит циклические колебания с периодом L;

– статистически значимый коэффициент автокорреляции первого порядка r(1) свидетельствует о наличии линейной тенденции в изучаемом процессе;

– периодические колебания в коэффициентах автокорреляции с лагом L говорят о наличии циклических процессов с периодом L;

– если среди всех вычисленных коэффициентов автокорреляции не оказалось ни одного существенного, т. е. все онистатистически неотличимы от нуля, то

либо ряд не содержит тенденции и циклических колебаний, а его уровни испытывают только случайные колебания около своего среднего значения (стационарный ряд),

либо ряд содержит сильную нелинейную тенденцию, выявление которой требует дополнительного анализа.

Вместе с тем важно понимать, что наличие в исследуемом ряде той или иной составляющей может проявляться не сразу, т. е. на исходных данных. Так, интенсивные периодические колебания могут заглушить слабый тренд. Поэтому, получив по коррелограмме вывод об отсутствии тренда, следует проверить его состоятельность после исключения из уровней ряда периодической составляющей. Зачастую тренд оказывается значимым, если он оценивается после исключения из уровней ряда сильных периодических колебаний.

Аналогично, для выявления слабой периодической составляющей анализируют корреляцию не исходных уровней, а их отклонений от тренда. При сопоставимой «силе» тренда и периодической составляющей они проявляются сразу на исходных данных.

Пример: в табл. 2 представлены квартальные данные об объемах продаж фирмы (млн долл.) за 4 года.

Таблица 2

Год

Квартал

y_t

Определим структуру временного ряда путём расчёта коэффициентов автокорреляции 1-го, 2-го, 3-го, 4-го порядков (при имеющихся наблюдениях(n = 16) L_max = n/4 = 16/4 = 4).

Чтобы найти коэффициент автокорреляции 1-го порядка, нужно оценить корреляцию между пятнадцатью парами наблюдений y_t и y_t₊₁ (t = 1, 2, …, 15).

y_t

y_t+₁

Проведём подготовительные расчёты для (23):

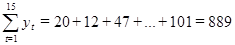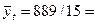; 59,27;

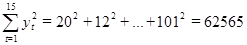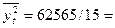; 4171;

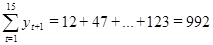; 66,13;

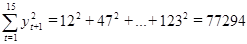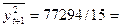; 5152,93;

; .

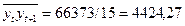Коэффициент автокорреляции 1-го порядка, согласно (23):

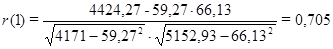Коэффициент автокорреляции 2-го порядка вычисляется по четырнадцати парам наблюдений y_t и y_t₊₂ (t = 1, 2, …, 14).

y_t

y_t+₂

Повторив приведённые выше расчёты для этих рядов, найдём коэффициент автокорреляции 2-го порядка: r(2) = 0,253.

Аналогично рассчитываются коэффициенты автокорреляции 3-го и 4-го порядков. Результаты расчета r(L) представим в виде таблицы (табл. 3) и коррелограммы (рис. 7).

Таблица 3

Лаг (порядок)	r(L)	Значимость
	0,705	значим
	0,253	незначим
	0,598	незначим
	0,996	значим

Рис. 7. Коррелограмма

Проверка коэффициентов автокорреляции на значимость при заданной величине α = 0,01 показала, что коэффициенты r(1) и r(4) статистически значимы, а коэффициенты r(2) и r(3) незначимы. При этом учитывали, что разным значениям лага L соответствуют разные критические точки распределения Стьюдента t(α/2;n). При вычислении r(1) учитывалось 15 уровней ряда, следовательно число степеней свободы n = 15 – 2 = 13. При вычислении r(2) учитывается 14 уровней ряда, следовательно n = 14 – 2 = 12, и т. д.

Вывод: статистически значимые коэффициенты автокорреляции r(1) и r(4) указывают на наличие в уровнях ряда линейной тенденции и сезонных колебанийс периодом в четыре квартала.