Линейная множественная регрессия
Цель: По опытным данным построить уравнение множественной линейной регрессии и определить его характеристики.
ПРИМЕР. Некоторая организация занимается торговлей компьютерами. Она определила, что на количество продаж основное влияние оказывают следующие факторы: цена товара 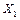 , затраты на рекламу
, затраты на рекламу 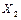 и число конкурирующих организаций в регионе
и число конкурирующих организаций в регионе  . Результаты наблюдений приведены в таблице
. Результаты наблюдений приведены в таблице
| Х1 | ||||||||||||||
| Х2 | ||||||||||||||
| Х3 | ||||||||||||||
| Y |
Построим линейное уравнение множественной регрессии. Для этого предварительно исследуем матрицу парных коэффициентов корреляции. Вводим исходные данные вместе с подписями в ячейки А1-О4. Для построения матрицы парной корреляции вызываем меню «Сервис/Анализ данных» (если пункт меню отсутствует, то вызываем «Сервис/Надстройки» и ставим галочку напротив строки «Пакет анализа»). Выбираем пункт «Корреляция». В появившемся окне в поле «Входной интервал» задаем ссылку на таблицу – А1-О4. Указываем группирование «По строкам». Ставим флажок в «Метки в первом столбце» (так как в ссылках на таблицу указаны подписи строк). В области «Параметры вывода» ставим флажок напротив «Выходной интервал» и напротив в поле даем ссылку на какую-либо ячейку, откуда будет осуществляться вывод данных, например А7. Нажимая «ОК», получаем нижнюю половину матрицы парной корреляции. Для общей оценки мультиколлинеарности факторов и адекватности регрессионной модели рассчитаем определители матриц 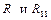 . Сформируем полную матрицу парных коэффициентов корреляции. В С8 задаем формулу «=В9», в D8 ссылку «=B10», в D9 – «=С10», в Е8 – «=В11», в Е9 – «=С11», в Е10 – «D11». Далее, для вычисления определителей в ячейку А13 вводим заголовок «
. Сформируем полную матрицу парных коэффициентов корреляции. В С8 задаем формулу «=В9», в D8 ссылку «=B10», в D9 – «=С10», в Е8 – «=В11», в Е9 – «=С11», в Е10 – «D11». Далее, для вычисления определителей в ячейку А13 вводим заголовок «  =» и в В13 ставим курсор и задаем функцию «МОПРЕД» (категория «Математические»), в которой аргумент «Массив» является ссылкой на ячейки B8:E11. В ячейку А14 вводим заголовок «
=» и в В13 ставим курсор и задаем функцию «МОПРЕД» (категория «Математические»), в которой аргумент «Массив» является ссылкой на ячейки B8:E11. В ячейку А14 вводим заголовок «  =» и в В14 ставим курсор и задаем функцию «МОПРЕД» с аргументом «Массив» - ссылкой на B8:D10. Результат - 0,427104 (ближе к 0, чем к 1), что говорит о достаточно высокой общей мультикорреляции. Найдем теперь коэффициент множественной корреляции. В А15 вводим «Rх=», а в В15 формулу «=КОРЕНЬ(1-В13/В14)». Результат 0,883788 говорит о достаточно высокой связи между фактором и функцией отклика.
=» и в В14 ставим курсор и задаем функцию «МОПРЕД» с аргументом «Массив» - ссылкой на B8:D10. Результат - 0,427104 (ближе к 0, чем к 1), что говорит о достаточно высокой общей мультикорреляции. Найдем теперь коэффициент множественной корреляции. В А15 вводим «Rх=», а в В15 формулу «=КОРЕНЬ(1-В13/В14)». Результат 0,883788 говорит о достаточно высокой связи между фактором и функцией отклика.
Проведем теперь отбор факторов. Рассмотрим матрицу коэффициентов парной корреляции. Видно, что 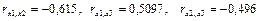 . Факторы можно считать коллинеарными (интеркоррелированными), если их парный коэффициент по модулю больше 0,7. В нашем случае таких пар факторов нет. Все факторы можно считать независимыми друг от друга и использовать в регрессионном уравнении. Определим теперь влияние каждого фактора
. Факторы можно считать коллинеарными (интеркоррелированными), если их парный коэффициент по модулю больше 0,7. В нашем случае таких пар факторов нет. Все факторы можно считать независимыми друг от друга и использовать в регрессионном уравнении. Определим теперь влияние каждого фактора 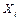 на функцию отклика Y. Для этого рассмотрим коэффициенты парной корреляции
на функцию отклика Y. Для этого рассмотрим коэффициенты парной корреляции  . Видно, что третий коэффициент -0,45 намного меньше по модулю, чем примерная граница 0,7, поэтому влияние третьего фактора Х3 на результат мало и его можно отбросить из рассмотрения.
. Видно, что третий коэффициент -0,45 намного меньше по модулю, чем примерная граница 0,7, поэтому влияние третьего фактора Х3 на результат мало и его можно отбросить из рассмотрения.
Копируем теперь на А18-О20 функцию отклика и значимые факторы (1, 2 и 4 строки, соответственно А1-О2 копируем в А18-О19, а А4-О4 – в А20-О20). В ячейку А22 вводим заголовок «Линейная» и в соседнюю В22 вводим функцию, определяющую параметры линейной регрессии «=ЛИНЕЙН» (категория «Статистические»). Аргументы функции: «Изв_знач_у» - B20:O20 (значения функции), «Изв_знач_х» - B18:O19 (значения двух значимых аргументов), «Константа» – 1 (расчет свободного члена), «Стат» - 1 (вывод дополнительных характеристик регрессии). Результат вычислений функции ЛИНЕЙН в случае функции нескольких переменных  имеет вид:
имеет вид:
| Коэффициент аk | Коэффициент ak-1 | … | Коэффициент 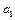
| Коэффици-ент 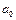
|
Стандартная ошибка 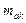
| Стандартная ошибка 
| … | Стандартная ошибка 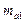
| Стандартная ошибка 
|
Коэффициент детерминации 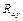
| Среднеквадратическое отклонение у | … | нет данных | нет данных |
| F – статистика | Степень свободы п-k-1 | … | нет данных | нет данных |
Регрессионная сум-ма квадратов 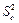
| Остаточная сумма квадратов 
| … | нет данных | нет данных |
В нашем случае имеем два фактора  , поэтому обводим 5 строк и три столбца В22-D26 и нажимаем F2 и Ctrl+Shift+Enter.
, поэтому обводим 5 строк и три столбца В22-D26 и нажимаем F2 и Ctrl+Shift+Enter.
Первая строка результата – значения параметров регрессионного уравнения 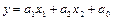 - числа
- числа 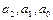 . Следовательно, уравнение регрессии есть
. Следовательно, уравнение регрессии есть  . Вторая строка – стандартные ошибки коэффициентов. Все они меньше самих коэффициентов, это значит, что коэффициенты значимы. В ячейках D24-D26 стоят значения «#Н/Д» (нет данных), как и должно быть в соответствии с таблицей.
. Вторая строка – стандартные ошибки коэффициентов. Все они меньше самих коэффициентов, это значит, что коэффициенты значимы. В ячейках D24-D26 стоят значения «#Н/Д» (нет данных), как и должно быть в соответствии с таблицей.
Коэффициент детерминации равен 0,7783. Видно, что F-критерий регрессионной модели равен 19,3097. Проверим модель на адекватность. Вычислим критическое значение статистики. Вводим в ячейку Н22 подпись «F-критическое» а в I22 вводим функцию FРАСПОБР, имеющую аргументы: «Вероятность» – уровень значимости, если он не задан в условии (как в нашем случае), то обычно его принимаем 0,05. Аргумент «Степени_свободы_1» - число независимых переменных (у нас их две -  ). Аргументом «Степени_свободы_2» служит число, показанное в ячейке С25 (в данном примере – 11). Видно, что F-статистика больше ее критического значения, поэтому модель адекватна.
). Аргументом «Степени_свободы_2» служит число, показанное в ячейке С25 (в данном примере – 11). Видно, что F-статистика больше ее критического значения, поэтому модель адекватна.
Задание на самостоятельную работу
Задание 1. Построить двухфакторную модель по данным
| Х1 | ||||||||||
| Х2 | ||||||||||
| Вар. | Значения Y (по вариантам) | |||||||||
| 1. | 38,1 | 38,6 | 40,9 | 38,6 | 41,3 | 43,1 | 44,3 | 43,0 | 45,8 | 46,2 |
| 2. | 30,8 | 31,1 | 30,4 | 31,7 | 30,5 | 33,5 | 31,0 | 34,5 | 36,0 | 32,9 |
| 3. | 10,7 | 11,0 | 13,2 | 12,4 | 13,2 | 13,3 | 14,4 | 15,3 | 14,8 | 14,8 |
| 4. | 23,7 | 24,8 | 25,8 | 27,6 | 26,9 | 25,2 | 26,6 | 26,3 | 29,0 | 30,4 |
| 5. | 22,8 | 26,3 | 28,0 | 26,1 | 26,0 | 29,9 | 30,9 | 32,9 | 33,9 | 33,5 |
| 6. | 26,5 | 26,4 | 28,2 | 26,7 | 29,1 | 29,7 | 29,7 | 31,2 | 32,1 | 32,4 |
| 7. | 25,3 | 28,8 | 30,1 | 30,0 | 32,5 | 31,4 | 32,0 | 36,4 | 35,6 | 36,9 |
| 8. | 10,0 | 9,7 | 11,6 | 12,2 | 13,3 | 13,9 | 15,6 | 16,7 | 15,1 | 16,8 |
| 9. | 20,9 | 20,7 | 20,8 | 20,9 | 22,8 | 22,4 | 24,5 | 22,9 | 22,7 | 24,6 |
| 10. | 24,8 | 26,5 | 28,3 | 29,1 | 27,0 | 28,4 | 30,0 | 32,4 | 32,0 | 32,3 |
| 11. | 29,4 | 30,0 | 32,0 | 33,1 | 32,6 | 33,9 | 33,6 | 35,0 | 34,7 | 35,9 |
| 12. | 20,3 | 20,4 | 22,1 | 24,3 | 25,1 | 25,1 | 26,9 | 25,4 | 27,8 | 26,9 |
| 13. | 20,8 | 20,2 | 21,5 | 21,8 | 24,4 | 23,7 | 25,7 | 24,7 | 27,2 | 24,8 |
| 14. | 28,6 | 28,6 | 28,8 | 29,2 | 31,7 | 32,7 | 32,1 | 33,3 | 33,8 | 35,0 |
| 15. | 16,1 | 17,0 | 20,5 | 17,1 | 18,8 | 21,0 | 22,7 | 24,2 | 23,4 | 26,7 |
Задание 2. Отобрать факторы и построить регрессионную модель для данных (для всех вариантов).
return false">ссылка скрыта| Х1 | |||||||||||||
| Х2 | |||||||||||||
| Х3 | |||||||||||||
| Х4 | |||||||||||||
| Y |
проверить значимость модели на уровне 0,01.