Доказательство.
Пусть  - всех корней
- всех корней  - ой степени из единицы. Очевидно, что
- ой степени из единицы. Очевидно, что 

 . Тогда
. Тогда  замкнуто относительно умножения.
замкнуто относительно умножения.
Операция умножения во множестве  ассоциативна;
ассоциативна;  - нейтральный элемент в
- нейтральный элемент в  ;
;  .
.
Таким образом,  группа, в которой элемент
группа, в которой элемент  является порождающим, так как
является порождающим, так как 
 , следовательно,
, следовательно,  - мультипликативная циклическая группа.
- мультипликативная циклическая группа.
что и требовалось доказать.
Определение. Комплексное число  называется корнем
называется корнем  - ой степени из ненулевого комплексного числа
- ой степени из ненулевого комплексного числа  , где
, где  , если
, если  .
.
Вычислим все корни  - ой степени из комплексного числа
- ой степени из комплексного числа  . Пусть
. Пусть  ,
,  . Зная, что
. Зная, что  , составим систему:
, составим систему:  . Тогда
. Тогда  и любой корень
и любой корень  - ой степени из комплексного числа
- ой степени из комплексного числа  будет иметь вид:
будет иметь вид:  .
.
Покажем, что существует ровно  различных корней
различных корней  - ой степени из комплексного числа
- ой степени из комплексного числа  . Для этого поделим
. Для этого поделим  на
на  с остатком, получим
с остатком, получим  , где
, где  . Следовательно,
. Следовательно, 
 . Поскольку
. Поскольку 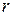 может принимать только одно из
может принимать только одно из  значений
значений  , то и различных корней
, то и различных корней  - ой степени из комплексного числа
- ой степени из комплексного числа  также будет ровно
также будет ровно  штук, причем
штук, причем  , где
, где  .
.
Замечание.Для каждого  справедливо
справедливо 
 .
.
Следствие.Все корни - ой степени из ненулевого комплексного числа
- ой степени из ненулевого комплексного числа  являются результатом умножения одного из этих корней на корни
являются результатом умножения одного из этих корней на корни  - ой степени из единицы.
- ой степени из единицы.
Пример. Найти все корни 3 – ей степени из -8.
Очевидно, что -2 – один из искомых корней. Тогда, согласно вышеприведенному следствию,
 ,
,
 ,
,
 .
.
Теорема 5.Полекомплексных чисел не является упорядоченным.