Доказательство.
Пусть  . Последнее означает, что
. Последнее означает, что
 - положительная, следовательно,
- положительная, следовательно,  .
.
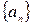 - ф.п.р.ч., следовательно,
- ф.п.р.ч., следовательно, 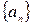 - ограниченная, тогда следовательно,
- ограниченная, тогда следовательно,  . Поскольку поле рациональных чисел архимедовски расположенное,
. Поскольку поле рациональных чисел архимедовски расположенное,  .
.
 .
.
что и требовалось доказать.
Теорема 6. Поле действительных чисел является всюду плотным.
Доказательство.
Пусть  . Для определенности положим, что
. Для определенности положим, что  . Тогда
. Тогда  - положительная, следовательно,
- положительная, следовательно,  . Поскольку
. Поскольку 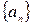 ,
,  - ф.п.р.ч, имеем
- ф.п.р.ч, имеем
 . Возьмем
. Возьмем  . Учитывая выше изложенное, получим
. Учитывая выше изложенное, получим

что и требовалось доказать.