И их свойства.
Эквивалентные последовательности рациональных чисел
Определение. Две фундаментальные последовательности рациональных чисел 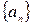
 называются эквивалентными, если
называются эквивалентными, если  является нулевой последовательностью, иначе
является нулевой последовательностью, иначе  .
.
Теорема 5.Отношение ≈ на множестве всех фундаментальных последовательностей рациональных чисел является отношением эквивалентности.
Доказательство.
Обозначим множество всех последовательностей рациональных чисел через  .
.
1. Рефлективность (?)

 .
.
2. Симметричность (?)
 3. Транзитивность (?)
3. Транзитивность (?)
 .
.
что и требовалось доказать
Теорема 6. Любая подпоследовательность фундаментальной последовательности эквивалентна ей.
Доказательство.
Пусть 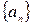 - ф.п.р.ч.,
- ф.п.р.ч.,  - произвольная подпоследовательность последовательности
- произвольная подпоследовательность последовательности 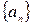 . Тогда
. Тогда 
 - монотонно возрастающая функция на множестве натуральных чисел. Покажем, что
- монотонно возрастающая функция на множестве натуральных чисел. Покажем, что  .
.
В силу фундаментальности последовательности 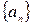 имеем
имеем  . Учитывая это, получим
. Учитывая это, получим
 .
.
что и требовалось доказать
Теорема 7. Фундаментальная последовательность рациональных чисел, эквивалентная нулевой, положительной, отрицательной является соответственно нулевой, положительной, отрицательной.