Примеры задач к теме 9

Задание 10

Проверьте возможность идентификации этой модели. Укажите какие переменные являются экзогенными, а какие эндогенными. Каким методом можно найти параметры структурной формы. Составьте приведенную форму модели.

Функция дохода:

Функция инвестиций:

Функция потребления: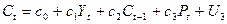

Функция прибыли: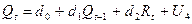

где – национальный доход периодов t и t–1;

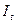– чистые инвестиции периода t;

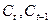– личное потребление периодов t, t–1;

– прибыль периодов t, t–1;

– индекс стоимости жизни периода t;

– индекс производительности в промышленности;

– случайные ошибки.

Задание 11

Проверьте возможность идентификации этой модели. Укажите, какие переменные являются экзогенными, а какие эндогенными. Каким методом можно найти параметры структурной формы. Составьте приведенную форму модели.

Функция денежного рынка:

Функция товарного рынка: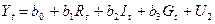

Функция инвестиций:

где – процентная ставка в период t;

– реальный валовый национальный доход в период t;

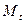– денежная масса в период t;

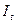– внутренние инвестиции в период t;

– реальные государственные расходы в период t;

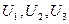– случайные ошибки.

Задание 12

Проверьте возможность идентификации этой модели. Укажите, какие переменные являются экзогенными, а какие эндогенными. Каким методом можно найти параметры структурной формы. Составьте приведенную форму модели.

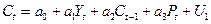
I_t = b₀ + b₁r_t + b₂I_t-1 + U₂

r_t = c₀+ c₁Y_t + c₂M_t + U₃

Y_t = C_t + I_t + G_t

где C – расходы на потребление;

Y – ВВП;

I – инвестиции;

r – процентная ставка;

M – денежная масса;

G – государственные расходы;

t, t–1 – текущий и предыдущий период;

U₁, U₂, U₃ – случайная компонента.

Задание 13

Проверьте возможность идентификации этой модели. Укажите, какие переменные являются экзогенными, а какие эндогенными. Каким методом можно найти параметры структурной формы. Составьте приведенную форму модели.

Y_t = a₀ + a₁Y_t + a₂I_t + U₁

I_t = b₀ + b₁Y_t + b₂Q_t + U₂

C_t = c₀ + c₁Y_t + c₂C_t-1 + c₃P_t + U₃

Q_t = d₀ + d₁Q_t-1 + d₂R_t + U₄

где Y – национальный доход;

C – расходы на личное потребление;

I – чистые инвестиции;

Q – валовая прибыль экономики;

P – индекс стоимости жизни;

R – объем продукции промышленности;

t – текущий период;

t–1 – предыдущий период,

U₁, U₂, U₃, U₄ – случайные ошибки.

Задание 14

Проверьте возможность идентификации этой модели. Укажите, какие переменные являются экзогенными, а какие эндогенными. Каким методом можно найти параметры структурной формы. Составьте приведенную форму модели.

Функция потребления: C_t = a₀ + a₁Y_t + a₂C_t-1 + U₁

Функция инвестиций: I_t = b₀ + b₁Y_t + b₂r_t + U₂

Функция денежного рынка: r_t = c₀ + c₁Y_t + c₂M_t + c₃r_t-1 + U₃

Тождество дохода: Y_t = C_t + I_t + G_t

где C – потребление;

Y – ВВП;

I – инвестиции;

r – процентная ставка;

M – денежная масса;

G – государственные расходы;

t, t–1 – текущий и предыдущий периоды;

U₁, U₂, U₃ – случайные ошибки.

Задание 15

Проверьте возможность идентификации этой модели. Укажите, какие переменные являются экзогенными, а какие эндогенными. Каким методом можно найти параметры структурной формы. Составьте приведенную форму модели.

функция денежного рынка: R_t = a₀ + a₁Y_t + a₂M_t + U₁

Функция товарного рынка: Y_t = b₀ + b₁R_t + b₂I_t + b₃G_t + U₂

Функция инвестиций: I_t = c₀ + c₁R_t + U₃

где R – процентные ставки;

Y – реальный ВВП;

M – денежная масса;

I – внутренние инвестиции;

G – реальные государственные расходы;

U₁, U₂, U₃ – случайные ошибки.

Задание 16

Проверьте возможность идентификации этой модели. Укажите, какие переменные являются экзогенными, а какие эндогенными. Каким методом можно найти параметры структурной формы. Составьте приведенную форму модели.

C_t = a₀ + a₁D_t + U₁

I_t = b₀ + b₁Y_t + b₂Y_t-1 + U₂

Y_t = D_t + T_t

D_t = C_t + I_t + G_t

где C – расходы на потребление;

Y – чистый национальный продукт;

D – чистый национальный доход;

I – инвестиции;

T – косвенные налоги;

G – государственные расходы;

t, t–1 – текущий и предыдущие периоды;

U₁, U₂ – случайные ошибки.

Задание 17

Проверьте возможность идентификации этой модели. Укажите, какие переменные являются экзогенными, а какие эндогенными. Каким методом можно найти параметры структурной формы. Составьте приведенную форму модели.

C_t = a₀ + a₁S_t + a₂P_t + U₁

S_t = b₀ +b₁R_t + b₂R_t-1 + b₃t + U₂

R_t = S_t + P_t

где C_t – личное потребление в период t;

S_t – зарплата в период t;

P_t – прибыль в период t;

R_t, R_t-1 – общий доход в период t и t–1;

U₁, U₂ – случайные ошибки.

Задание 18

Проверьте возможность идентификации этой модели. Укажите, какие переменные являются экзогенными, а какие эндогенными. Каким методом можно найти параметры структурной формы. Составьте приведенную форму модели.

C_t = a₀ + a₁Y_t + a₂I_t + U₁

I_t = b₀ + b₁Y_t-1 + U₂

T_t = c₀ + c₁Y_t + U₃

Y_t = C_t + I_t + G_t

где C_t – совокупное потребление в период t;

Y_t, Y_t-1 – совокупный доход в периоды t и t–1;

I_t – инвестиции в период t;

T_t – налоги в период t;

G_t – государственные доходы в период t;

U₁, U₂, U₃ – случайные ошибки.

Варианты тестов

Тест 1

1.1. Какое определение соответствует понятию «эконометрика»:

это наука, предметом изучения которой является количественная сторона массовых социально-экономических явлений и процессов в конкретных условиях места и времени;

это наука, предметом изучения которой является количественное выражение взаимосвязей экономических явлений и процессов;

это наука, предметом изучения которой являются общие закономерности случайных явлений и методы количественной оценки влияния случайных факторов.

1.2. Какова цель эконометрики:

представить экономические данные в наглядном виде;

разработать способы моделирования и количественного анализа реальных экономических объектов;

определить способы сбора и группировки статистических данных;

изучить качественные аспекты экономических явлений.

1.3. Спецификация модели – это:

определение цели исследования и выбор экономических переменных модели;

проведение статистического анализа модели, оценка качества ее параметров;

сбор необходимой статистической информации;

построение эконометрических моделей с целью эмпирического анализа.

1.4. Какая задача эконометрики является задачей параметризации модели:

составление прогноза и рекомендаций для конкретных экономических явлений по результатам эконометрического моделирования;

оценка параметров построения модели;

проверка качества параметров модели и самой модели в целом;

построение эконометрических моделей для эмпирического анализа.

1.5. Верификация модели – это:

определение вида экономической модели, выражение в математической форме взаимосвязи между ее переменными;

определение исходных предпосылок и ограничений модели;

проверка качества как самой модели в целом, так и ее параметров;

анализ изучаемого экономического явления.

1.6. Из перечисленных моделей выберите регрессионные модели с одним уравнением:

модель цены от объема поставки;

модель спроса и предложения;

модель тренда и сезонности;

модель зависимости объема производства от производственных факторов.

Набор сведений о разных объектах, взятых за один период времени, называется:

временными данными;

пространственными данными.

1.7. Выберите аналог понятия «независимая переменная»:

эндогенная переменная;

фактор;

результат;

экзогенная переменная.

1.8. Рассмотрите модель зависимости общей величины расходов на питание от располагаемого личного дохода (x) и цены продуктов питания (p): . Определите класс модели и вид переменных модели:

регрессионная модель с одним уравнением; эндогенная переменная – расходы на питание, экзогенная переменная – располагаемый личный доход, предопределенная переменная – цена продуктов питания;

регрессионная модель с одним уравнением; эндогенная переменная – расходы на питание, экзогенные переменные – располагаемый личный доход и цена продуктов питания;

модель временного ряда; эндогенная переменная – расходы на питание, лаговые переменные – располагаемый личный доход и цена продуктов питания.

1.9. Найдите правильную последовательность этапов эконометрического моделирования:

постановочный, априорный, параметризации, информационный, идентификации, верификации;

постановочный, априорный, информационный, параметризации, идентификации, верификации;

информационный, постановочный, априорный, параметризации, верификации, идентификации.

Тест 2

2.1. Связь называется корреляционной:

если каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного признака;

если каждому значению факторного признака соответствует множество значений результативного признака, то есть определенное статистическое распределение;

если каждому значению факторного признака соответствует целое распределение значений результативного признака;

если каждому значению факторного признака соответствует строго определенное значение факторного признака;

2.2. По аналитическому выражению различают связи:

обратные;

линейные;

криволинейные;

парные.

2.3. Регрессионный анализ заключается в определении:

аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимает постоянные, как правило, средние значения;

тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи);

статистической меры взаимодействия двух случайных переменных;

степени статистической связи между порядковыми переменными.

2.4. Под частной корреляцией понимается:

зависимость результативного признака и двух и более факторных признаков, включенных в исследование;

связь между двумя признаками (результативным и факторным или двумя факторными);

зависимость между результативным и одним факторным признаками при фиксированных значениях других факторных признаков;

зависимость между качественными признаками.

2.5. Какие значения не может принимать парный коэффициент корреляции:

–0,973;

+0,005;

+1,111;

+0,721.

2.6. При каком значении линейного коэффициента корреляции связь между признаками Y и X можно считать тесной (сильной):

–0,975;

+0,657;

-0,111;

+0,421.

2.7. Какой критерий используется для оценки значимости коэффициента корреляции:

F – критерий Фишера;

t – критерий Стъюдента;

критерий Пирсона;

– критерий Дарбина – Уотсона.

2.8. Если парный коэффициент корреляции между признаками Y и X равен –1, то это означает:

отсутствие связи;

наличие обратной корреляционной связи;

наличие обратной функциональной связи;

наличие прямой функциональной связи.

2.9. Если парный коэффициент корреляции между признаками Y и X принимает значение 0,675, то коэффициент детерминации равен:

0,822;

–0,675;

0,576;

0,456.

2.10. Согласно методу наименьших квадратов минимизируется следующее выражение:

;

;

;

.

2.11. Оценки параметров регрессии (свойства оценок МНК) должны быть:

несмещенными;

гетероскедастичными;

эффективными;

состоятельными.

2.12. В уравнении линейной парной регрессии параметр a означает:

усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов;

среднее изменение результативного признака при изменении факторного признака на 1%;

на какую величину в среднем изменится результативный признак y, если переменную x увеличить на единицу измерения;

какая доля вариации результативного признака y учтена в модели и обусловлена влиянием на нее переменной x.

2.13. Значение параметра в уравнении линейной парной регрессии определяется по формуле

;

;

;

.

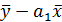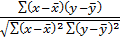2.14. Уравнение регрессии имеет вид: . На сколько единиц своего измерения в среднем изменится при увеличении на одну единицу своего измерения:

увеличится на 2,02;

увеличится на 0,78;

увеличится на 2,80;

не изменится.

2.15. Какой критерий используют для оценки значимости уравнения регрессии:

F – критерий Фишера;

t – критерий Стъюдента;

критерий Пирсона;

– критерий Дарбина – Уотсона.

2.16. Какой коэффициент определяет среднее изменение результативного признака при изменении факторного признака на 1%:

коэффициент регрессии;

коэффициент детерминации;

коэффициент корреляции;

коэффициент эластичности.

2.17. Чему равенкоэффициент эластичности, если уравнение регрессии имеет вид , а :

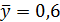0,94;

1,68;

0,65;

2,42.

2.18. Уравнение степенной функции имеет вид:

;

;

;

.

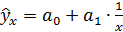2.19. Уравнение гиперболы имеет вид:

;

;

;

.

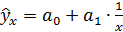2.20. Индекс корреляции определяется по формуле:

;

;

;

.

 

Тест 3

3.1. В каких пределах изменяется множественный коэффициент корреляции:

;

;

.

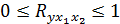3.2. В каких пределах изменяется множественный коэффициент детерминации:

;

;

.

3.3. Частный коэффициент корреляции оценивает:

тесноту связи между двумя переменными;

тесноту связи между тремя переменными;

тесноту связи между двумя переменными при фиксированном значении остальных факторов.

3.4. Какой коэффициент указывает в среднем процент изменения результативного показателя y при увеличении аргумента x на 1%:

коэффициент детерминации;

коэффициент регрессии;

коэффициент эластичности;

бета-коэффициент.

3.5. Множественный линейный коэффициент корреляции равен 0,75. Какой процент вариации зависимой переменной y учтен в модели и обусловлен влиянием факторов и :

56,2;

75,0;

37,5.

3.6. Имеются следующие данные:

коэффициент регрессии = 1,341;

среднее квадратичное отклонение коэффициента регрессии = 0,277.

Определите t-критерий Стъюдента и оцените значимость коэффициента регрессии , если = 2,11 при уровне значимости = 0,05:

0,207 – коэффициент незначим;

4,841 – коэффициент значим;

4,841 – коэффициент незначим.

3.7. Имеется матрица парных коэффициентов корреляции:

	–0,782
	0,451	0,564
	0,842	–0,873	0,303

Между какими признаками наблюдается мультиколлинеарность:

и ;

и ;

и .

3.8. Какое значение может принимать множественный коэффициент корреляции:

1,501;

–0,453;

0,861.

3.9. Уравнение множественной регрессии имеет вид:

. Параметр = 1,37 означает следующее:

при увеличении на одну единицу своего измерения переменная y увеличится на 1,37 единиц своего измерения;

при увеличении на одну единицу своего измерения и при фиксированном значении фактора переменная y увеличится на 1,37 единиц своего измерения;

при увеличении на 1,37 единиц своего измерения и при фиксированном значении фактора переменная y увеличится на одну единицу своего измерения.

3.10. Значение бета-коэффициента определяется по формуле:

;

;

.

Тест 4

4.1. Системами эконометрических уравнений являются:

системы одновременных уравнений;

системы рекурсивных уравнений;

системы нормальных уравнений;

системы независимых уравнений.

4.2. Система одновременных уравнений отличается от других видов эконометрических систем тем, что в ней:

эндогенная переменная одного уравнения находится в другом уравнении системы в качестве фактора;

одни и те же эндогенные переменные системы в одних уравнениях находятся в левой части, а в других уравнениях – в правой части;

каждая эндогенная переменная является функцией одной и той же совокупности экзогенных переменных.

4.3. МНК позволяет получить состоятельные и несмещенные оценки параметров системы:

рекурсивных уравнений;

одновременных уравнений;

независимых уравнений.

4.4. Экзогенные переменные модели характеризуются тем, что они:

датируются предыдущими моментами времени;

являются независимыми и определяются вне системы;

являются зависимыми и определяются внутри системы.

4.5. Выберите аналог понятия «эндогенная переменная»:

результат;

фактор;

зависимая переменная, определяемая внутри системы;

предопределенная переменная.

4.6. Для данной приведенной формы модели

укажите соответствующую ей структурную форму:

 

 

4.7. Если структурные коэффициенты модели выражены через приведенные коэффициенты и имеют более одного числового значения, то такая модель:

сверхидентифицируемая;

неидентифицируемая;

идентифицируемая.

4.8. Количество структурных и приведенных коэффициентов одинаково в модели:

сверхидентифицируемой;

неидентифицируемой;

идентифицируемой.

4.9. Изучите взаимосвязь переменных в системе одновременных уравнений:

где:

– расходы на потребление в период t;

– расходы на потребление в период (t-1);

– инвестиции в период t;

– инвестиции в период (t-1);

– процентная ставка в период t;

– совокупный доход в период t;

– денежная масса в период t;

– расходы государства в период t;

– текущий период;

−1) – предыдущий период.

Найдите предопределенные переменные (1), эндогенные переменные (2), экзогенные переменные (3), лаговые эндогенные переменные (4) среди совокупностей:

а) инвестиции в период −1); расходы на потребление в период −1);

б) денежная масса в период t; расходы государства в период t;

в) расходы на потребление в период t; инвестиции в период t; процентная ставка в период t; совокупный доход в период t;

г) денежная масса в период t; инвестиции в период (t–1); расходы государства в период t; расходы на потребление в период (t–1).

4.10. В структурной модели, см. тестовое задание 4.9, не требует проверки на идентификацию равенство, описывающее зависимость:

расходов на потребление в период t от совокупного дохода в период t и расходов на потребление в период (t-1);

инвестиций в период t от процентной ставки в период t и от инвестиций в период (t–1);

совокупного дохода в период t от расходов государства, расходов на потребление и инвестиций в такой же период t;

процентной ставки в период t от совокупного дохода и денежной массы в такой же период t.

4.11. Проверили на идентифицируемость одно из уравнений модели:

где:

– расходы на потребление в период t;

– расходы на потребление в период (t-1);

– инвестиции в период t;

– инвестиции в период (t-1);

– процентная ставка в период t;

– совокупный доход в период t;

– денежная масса в период t;

– расходы государства в период t;

– текущий период;

−1) – предыдущий период.

Получили, что в этом уравнении находятся две эндогенные переменные (n=2) и отсутствуют три предопределенные переменные (p=3), то есть n<p+1. Достаточное условие идентификации для уравнений выполняется: определитель матрицы, составленный из коэффициентов при переменных, которых неит в этом уравнении, не равен нулю, и ранг этой матрицы равен 3. Таким образом, сверхидентифицируемым является:

уравнение (1);

уравнение (2);

уравнение (3);

уравнения (1)-(3) модели.

4.12. Определите, для какого уравнения структурной модели

выполняется необходимое условие идентифицируемости:

а) уравнение (1); n=2 ( и – эндогенные переменные в уравнении); p=2 ( и – экзогенные переменные, которых нет в уравнении);

б) уравнение (2); n=1 ( – эндогенная переменная в уравнении); p=1 ( – экзогенная переменная, которой нет в уравнении);

в) уравнение (3); n=2 ( и – эндогенные переменные в уравнении); p=1 ( – экзогенная переменная, которой нет в уравнении);

4.13. Доказано, что система одновременных уравнений

Идентифицируемая. Определите, какое обоснование идентифицируемости проведено для второго уравнения системы:

а) необходимое условие выполняется: n=3 ( , ); p=2 ( и ), значит n= p+1; достаточное условие выполняется:

(3)
(2)
(1)

, rang =2. Общий вывод: уравнение точно идентифицируемое;

б) необходимое условие выполняется: n=2 ( ); p=1 ( ), значит n= p+1; достаточное условие выполняется:

(2)
(1)
(3)	-1

, rang =2. Общий вывод: уравнение точно идентифицируемое;

в) необходимое условие выполняется: n=2 ( , ); p=1 ( ), значит n= p+1; достаточное условие выполняется:

(1)
(2)	-1
(3)

, rang =2. Общий вывод: уравнение точно идентифицируемое.

4.14. Приведенная форма модели имеет вид

Три студента вычисляли структурные коэффициенты, получили разные ответы. Определите, кто из них прав:

а)

б)

в)

4.15. Рассмотрите систему одновременных уравнений и соответствующую ей таблицу коэффициентов при переменных системы:

 

Уравнения	Переменные
эндогенные	предопределенные
(1)	–1
(2)		–1
(3)			–1

а) первое уравнение, при условии, что другие структурные уравнения системы идентифицируемые;

б) второе уравнение, при условии, что другие структурные уравнения системы идентифицируемые;

в) третье уравнение, при условии, что другие структурные уравнения системы идентифицируемые.

4.16. Упрощенный вариант макроэкономической модели Клейна имеет вид:

Где первое уравнение есть уравнение функции потребления, второе – уравнение инвестиций, третье – тождество;

– потребление в период t;

– национальный доход в период t;

– налоги на бизнес в период t;

– инвестиции;

– запас капитала в период (t-1).

В этой модели используется допущение, согласно которому экономика состоит только из частного сектора, государственного сектора экономики нет.

Подставьте тождество (3) в первое и второе уравнения модели Клейна и получите уравнения структурной формы, подлежащие оценке. Полученной структурной форме соответствует приведенная форма модели, которая имеет вид:

а)

б)

в)

4.17. Найдите правильную последовательность шагов алгоритма косвенного МНК:

а) I. Приведенная форма модели преобразуется в структурную форму.

II. Параметры структурной формы модели оцениваются с помощью МНК.

III. Структурная форма модели преобразуется в приведенную форму.

б) I. Параметры структурной формы модели оцениваются с помощью МНК.

II. Приведенная форма модели преобразуется в структурную форму.

III. Структурная форма модели преобразуется в приведенную форму.

в) I. Структурная форма модели преобразуется в приведенную форму.

II. Параметры структурной формы модели оцениваются с помощью МНК.

III. Приведенная форма модели преобразуется в структурную форму.

4.18. Экзогенные переменные модели характеризуются тем, что они:

а) датируются предыдущими моментами времени:

б) являются независимыми и определяются вне системы;

в) являются зависимыми и определяются внутри системы.

4.19. Найдите правильную последовательность шагов алгоритма применения двухшагового МНК:

а) I. Получение по соответствующим приведенным уравнениям теоретических значений эндогенных переменных правой части сверхидентифицируемого уравнения модели.

II. Процесс оценки параметров сверхидентифицируемого уравнения модели через теоретические значения эндогенных и фактические значения предопределенных переменных.

III. Преобразование структурной формы модели в приведенную.

IV. Процесс оценки параметров приведенной формы с помощью МНК;

б) I. Преобразование структурной формы модели в приведенную.

II. Процесс оценки параметров приведенной формы с помощью МНК.

III. Получение по соответствующим приведенным уравнениям теоретических значений эндогенных переменных правой части сверхидентифицируемого уравнения модели.

IV. Процесс оценки параметров сверхидентифицируемого уравнения модели через теоретические значения эндогенных и фактические значения предопределенных переменных;

в) I. Процесс оценки параметров приведенной формы с помощью МНК.

II. Получение по соответствующим приведенным уравнениям теоретических значений эндогенных переменных правой части сверхидентифицируемого уравнения модели.

III. Процесс оценки параметров сверхидентифицируемого уравнения модели через теоретические значения эндогенных и фактические значения предопределенных переменных.

4.19. Рассмотрите структурную форму и соответствующую ей таблицу коэффициентов при переменных модели:

 

Уравнения	Переменные
экзогенные	предопределенные
(1)	–1
(2)		–1
(3)			–1

Если к уравнению (1) системы применить двухшаговый МНК, то оценки параметров получатся:

а) состоятельными и несмещенными;

б) несостоятельными и смещенными.

4.20. Модель денежного рынка имеет вид:

где

– денежная масса;

– внутренние инвестиции;

– процентная ставка;

– ВВП;

– текущий период.

Можно утверждать, что оценки параметров, полученные двухшаговым МНК, совпадают с оценками, найденными косвенным МНК, если:

а) система идентифицируемая;

б) для каждого уравнения системы выполняется необходимое и достаточное условие идентифицируемости;

в) количество коэффициентов регрессии структурных уравнений совпадает с количеством коэффициентов регрессии приведенных уравнений.

Вопросы для подготовки к зачету

1. Эконометрика как наука. История развития эконометрики.

2. Предмет, цель и задачи эконометрики.

3. Эконометрическая модель – основа механизма эконометрического моделирования. Классы моделей.

4. Типы данных и виды переменных в эконометрических исследованиях экономических явлений.

5. Этапы эконометрического моделирования.

6. Понятие о детерминированных и стохастических процессах.

7. Статистическая зависимость (независимость) случайных переменных.

8. Понятие функциональной и статистической зависимостей.

9. Методы прогнозирования.

10. Спецификация эконометрических моделей.

11. Этапы проведения комплексного корреляционно-регрессионного анализа.

12. Регрессионная модель с одним уравнением и требования к ее построению.

13. Спецификация моделей парной регрессии.

14. Понятие о стандартной ошибке и оценке существенности коэффициентов регрессии.

15. Оценка параметров парной регрессии и их экономическая интерпретация.

16. Расчет и интерпретация коэффициента корреляции для парной линейной регрессии.

17. Коэффициент детерминации и его характеристика.

18. Дисперсионный анализ. Сущность и методика проведения.

19. Интервалы прогноза по линейному уравнению регрессии.

20. Средняя ошибка аппроксимации.

21. Нелинейные регрессии и их характеристика.

22. Статистическое изучение парной нелинейной регрессионной эконометрической модели.

23. Расчет индекса корреляции для парной нелинейной регрессии.

24. Отбор факторных признаков при построении множественной регрессии.

25. Оценка параметров множественной регрессии.

26. Множественная и частная корреляция.

27. Задачи множественного корреляционно-регрессионного анализа.

28. Понятие мультиколлинеарности и способы ее устранения.

29. Частный коэффициент корреляции.

30. t-критерий Стьюдента в оценке значимости коэффициента корреляции.

31. Понятие о коэффициенте эластичности и его характеристика.

32. Β-коэффициент линейной регрессии и его применение.

33. Индексы множественной корреляции и детерминации и их характеристика.

34. Прогнозирование по уравнению регрессии.

35. Предпосылки метода наименьших квадратов.

36. Общие понятия о системе одновременных уравнений и ее составляющие.

37. Формы представления системы одновременных уравнений.

38. Задачи идентификации уравнений системы. Необходимое и достаточное условие идентифицируемости.

39. Косвенный метод наименьших квадратов: алгоритм и условия его применения.

40. Двухшаговый метод наименьших квадратов: алгоритм и условия его применения.

41. Классы динамических эконометрических моделей и их характеристика.

42. Характеристика моделей с распределенным лагом и оценка их параметров.

43. Выбор формы модели с распределенным лагом.

44. Лаговые модели Алмон.

45. Гомоскедастичность и гетероскедастичность остатков.

46. Тесты проверки на гетероскедастичность и их характеристика.

47. Сущность обобщенного метода наименьших квадратов.

48. Временной ряд и его составляющие.

49. Моделирование временных рядов.

50. Аддитивная и мультипликативная модель временного ряда.

51. Моделирование тенденции временного ряда.

52. Основные типы трендов и их распознавание.

53. Выявление сезонной компоненты по временному ряду.

54. Выявление случайной компоненты по временному ряду.

55. Понятие автокорреляции и авторегрессии временного ряда. Виды автокорреляции.

56. Выявление автокорреляции остатков по критерию Дарбина-Уотсона.

57. Тестирование гипотезы о коинтеграции временных рядов. Критерий Энгеля-Грангера.

58. Методы коррелирования и проверка гипотезы о коинтеграции.

59. Ряд Фурье и его применение в оценке тренда.

60. Характеристика авторегрессионных моделей. Метод Койка.

61. Оценка параметров моделей авторегрессии методом инструментальной переменной.

62. Модели адаптивных ожиданий.

63. Модели частичной корректировки.