ЗАДАЧА № 1 Тема: Парная регрессия

Контрольная работа по дисциплине «Эконометрика»

1. Проведите качественный анализ связей экономических переменных, выделив зависимую и независимую переменные.

2. Постройте поле корреляции результата и фактора, сформулируйте гипотезу о виде связи (линейная или нелинейная; для нелинейной – конкретный вид)

3. Рассчитайте линейный коэффициент корреляции, определите его значимость при α=0,05.

4. Постройте интервальную оценку линейного коэффициента корреляции (с надежностью – 95%).

5. Определите параметры уравнения парной линейной регрессии и дайте интерпретацию коэффициента регрессии.

6. Рассчитайте параметры одной из функций регрессии (в соответствии с выдвинутой гипотезой (п.2):

· квадратичной;

· степенной;

· показательной;

· равносторонней гиперболы.

7. С вероятностью 0,95 оцените статистическую значимость каждого параметра и уравнений регрессии в целом.

8. Определите средние коэффициенты эластичности для каждой модели.

9. Отобразите на поле корреляций теоретически рассчитанные линии регрессии для каждой из моделей.

10. Рассчитайте для нелинейной модели индекс детерминации.

11. Постройте доверительную область для каждой модели.

12. Оцените качество построенных (пп. 5 и 7) моделей через среднюю относительную ошибку аппроксимации и F-критерий Фишера.

13. Выберете лучшую из моделей, выбор обоснуйте.

14. С вероятностью 0,95 постройте доверительный интервал ожидаемого значения результативного признака в предположении, что значение признака фактора увеличится на 5% относительно своего среднего уровня.

Вариант	Округ Признаки	Источник данных
	Приволжский федеральный округ РФ Выявить и оценить зависимость между расходованием средств пенсионного фонда за 2003 г. по субъектам РФ, млрд руб., (y₁₀) и поступлением средств в пенсионный фонд по субъектам РФ, млрд руб., x₁₀	ПАРНРЕГР.doc.

Таблица 1.1.

Исходные данные

Территории федерального округа	Расходование средств пенсионного фонда за 2003 г. по субъектам РФ, млрд руб., y₁₀	Поступление средств в пенсионный фонд по субъектам РФ за 2003 г., млрд руб., x₁₀
Республика Башкортостан	19,7	17,3
Республика Марий Эл	3,5	2,6
Республика Мордовия	4,9	3,6
Республика Татарстан	18,9	17,8
Республика Удмуртия	7,9	7,3
Чувашская республика	6,4	5,1
Кировская обл.	8,7	6,6
Нижегородская обл.	21,8	17,5
Оренбургская обл.	11,1	8,8
Пензенская обл.	8,5	5,7
Пермская обл.	15,3	14,1
Самарская обл.	18,2	17,0
Саратовская обл.	13,9	10,3
Ульяновская обл.	7,6	5,7

Решение

Отобразим данн6ые в таблице пакета Statistica 6.1:

Таблица 1.2

1) Первичной величиной является Поступление средств в пенсионный фонд по субъектам РФ, а по нему будет определяться Расходование средств пенсионного фонда. Поэтому в качестве независимой переменной возьмем Поступление средств в пенсионный фонд и обозначим ее через х (фактор). Расходование средств пенсионного фонда обозначим через у (результат).

2). Построим поле корреляции результата и фактора и сформулируем гипотезу о виде связи (линейная или нелинейная; для нелинейной – конкретный вид)

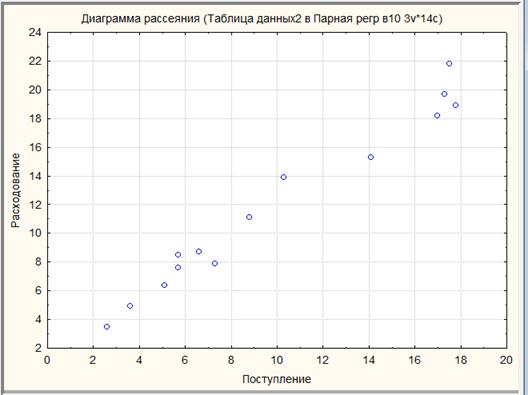
Рис. 1.1. Поле корреляции результата и фактора

По виду поля корреляции видно, что связь между переменными явно имеет линейный вид.

3. Найдем линейный коэффициент корреляции и определим его значимость при α=0,05.

Найдем для переменных х и у их средние значения, дисперсии и средние квадратические отклонения.

Таблица 1.3

Средние значения: = 9,957, = 11,886.

Дисперсии:

σ_x² = 31,789, σ_y² = 36,141 = 174,83–11,886² = 174,83–141,277 = 33,553

Средние квадратические отклонения:

σ_x = 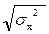= 5,6382, σ_y = = 6,0118

Найдем линейный коэффициент корреляции х и у:

Таблица 1.4

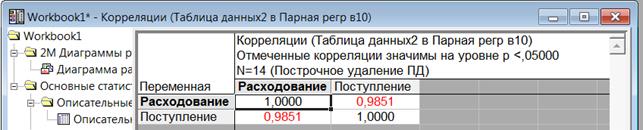
R_xy = = = = 0,9851

Определим его значимость при α=0,05 с помощью t-критерия:

Таблица 1.5

t_r = = = 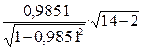= 19,855

Эта величина значительно превышает табличное значение t_α_,_n_–2 =t_{0,05; 12} =2,179,

Значит, коэффициент корреляции существенно отличен от нуля, и зависимость является значимой.

4. Построим интервальную оценку линейного коэффициента корреляции (с надежностью – 95%).

Ошибка коэффициента корреляции:

m_r = = = = = 0,0497

Предельная ошибка: Δ = t·σ_m

Доверительный интервал для среднего значения ν случайной величины Х для вероятности α=0,05:

(r–t m_r < R< r+t m_r) = (0,9851–2,179·0,0497 < R < 0,9851+2,179·0,0497) =

= (0,9851– 0,1083 < R < 0,9851+ 0,1083) = (0,8768 < R < 1,0934676),

т.е. интервал (0,8768; 1)

5. Параметры уравнения парной линейной регрессии y = a+bx были определены ранее (см. таблицу 4):

Таблица 1.6

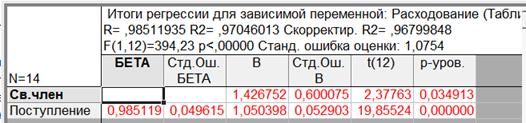
Коэффициенты регрессии: a = 1,426752, b = 1,0504

Табличное значение t_α_,_n_–2 = t_{0,05; 12} = 2,179 – меньше, чем в таблице для a и b.

Значит оба коэффициента значимы.

y = a+b∙x = 1,4272 + 1,0504∙x

Таблица 1.7

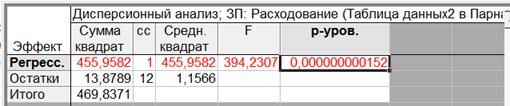
Выдвинем гипотезу H₀ о том, что построенное уравнение является надежным.

Фактическое значение F_Факт = F(1,52E-10;1;12)= 394,23.

F_Табл (0,05; 1; 12) = 4,75

Т.к. F_Факт < F_Табл, то делаем вывод , что гипотеза признается.

Ниже приведен график линейной регрессии.

Рис. 1.2. Линия линейной регрессии у на х

Интерпретация коэффициента регрессии b = 1,0504 заключается в том, что при увеличении х на 1 величина у увеличивается на 1,0504.

6. Рассчитаем параметры одной из функций регрессии (в соответствии с выдвинутой гипотезой (п.2):

· квадратичной;

· степенной;

· показательной;

· равносторонней гиперболы.

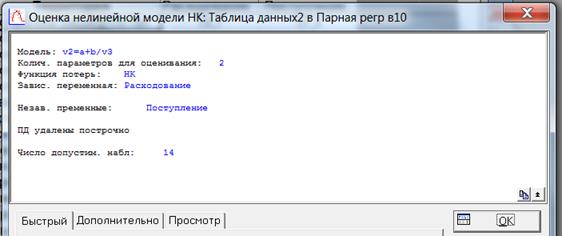
Для нелинейных моделей выбираемАнализ → Углубленные методы анализа → Нелинейное оценивание → Регрессия пользователя – метод наим. квадратов МНК. Появится окно «Оцениваемая функция», в котором набираем формулу нужной функции.

a) Построим квадратичную регрессию y = a+bx+cx².

Введем формулу v2=a+b*v3+c*v3^2:

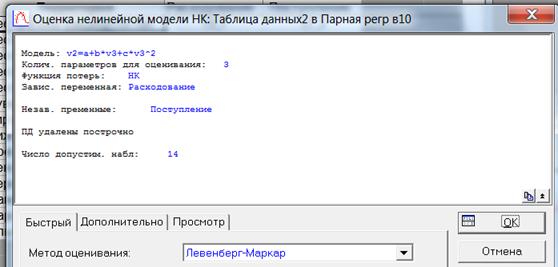
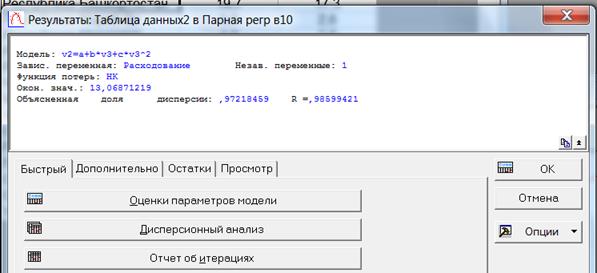
Выберем оценки параметров модели:

Уравнение квадратичной регрессии:

y = a+bx+cx² = 0,32196+1,32433x–0,01261х²

Коэффициенты а и c не значимы: t_a = 0,219, t_a = 0,8258 < t_{0,05; 11} = 2,202

Коэффициент b значим: t_a = 3,941 > t_{0,05; 11} = 2,202

В окне «Результаты» нажмем кнопку «Дисперсионный анализ»:

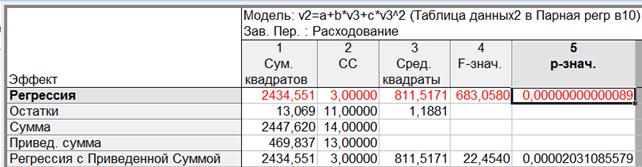
Рисунок 1.5 – Итоги дисперсионного анализа для линейной регрессии

Фактическое значение F_Факт = F(0,89E-12;3;11)=683,058.

F_Табл (0,05; 3;11) =3,59

Имеем F(0,89E-12;3;11) > F_Табл (0,05; 3; 11), то уравнение признается надежным.

Рис. 1.6. Линия квадратичной регрессии у на х

б) Построим теперь степенную регрессию y = ax^b.

Набираем формулу v2=a*v3^b:

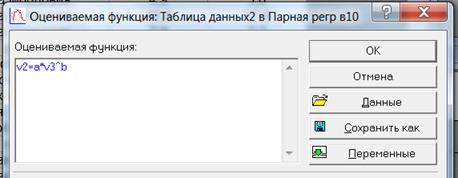
Рис. 1.7 – Итоги степенной регрессии

Получили степенную регрессию: y = 1,6751·x^0,860959

Коэффициенты а и b значимы: t_a = 7,39284, t_b = 16,785 > t_{0,05; 12} = 2,179

Рис. 1.8 – Итоги дисперсионного анализа для степенной регрессии

Выдвинем гипотезу H₀ о том, что построенное уравнение является надежным.

Фактическое значение F_Факт = F(0,23E-14;2;12)= 1116,876.

F_Табл (0,05; 2; 12) = 3,88

Проверив неравенство F_Факт > F_Табл, делаем вывод , что есть основания принимать гипотезу, и уравнение признается надежным.

Рис.1.9. Линия степенной регрессии у на х

в) Показательная функция у = α∙е^βх. Набираем формулу v2=a*exp(b*v3):

После нажатия ОК:

Выберем оценки параметров модели:

Рисунок 2.4 – Итоги показательной регрессии

Получили показательную функцию y = ae^b = 4,732064·e^0,082605^x

Коэффициенты а и b значимы: t_a = 9,85495, t_b = 12,39166 > t_{0,05; 12} = 2,179

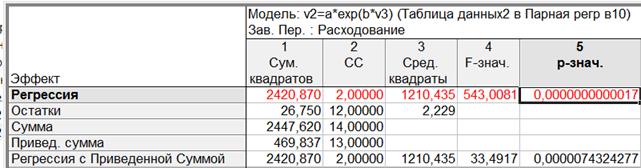
Рисунок 2.6 – Итоги дисперсионного анализа для экспоненциальной регрессии

Выдвинем гипотезу H₀ о том, что построенное уравнение является надежным.

Фактическое значение F_Факт = F(1,7E-12;2;12)= 543.

F_Табл (0,05; 2; 12) =3,88

Проверив неравенство F_Факт > F_Табл, делаем вывод , что нет основания отвергать гипотезу, и уравнение признается надежным.

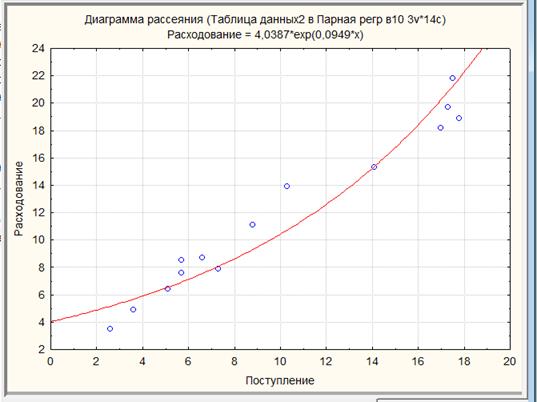
Рис.1.9. Линия показательной регрессии у на х

г) Равносторонняя гипербола y = a + 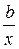. Вводим формулу v2=a+b/v3:

Гиперболическая регрессия y = 19,7069 –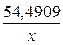

Коэффициенты а и b значимы: t_a = 12,78766, t_b = 6,03181 > t_{0,05; 12} = 2,179

Получили гиперболическую регрессию: y = 1,6751·x^0,860959

Коэффициенты а и b значимы: t_a = 7,39284, t_b = 16,785 > t_{0,05; 12} = 2,179

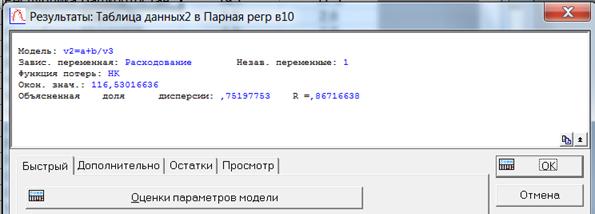
Рисунок 1.10 – Итоги дисперсионного анализа для гиперболической регрессии

Фактическое значение F_Факт = F(0,0000000116;2;12)= 120,025.

F_Табл (0,05; 2; 12) =3,88

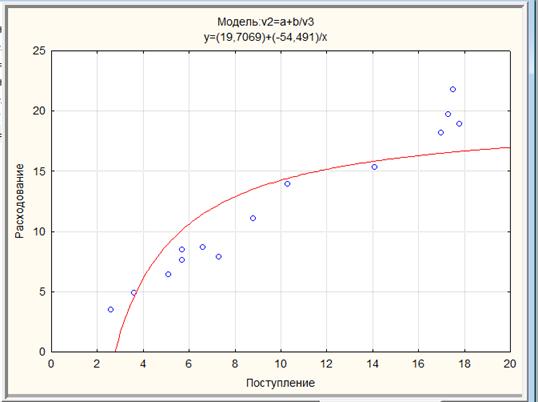
Рис. 1.11. Линия гиперболической регрессии у на х

5. Рассчитаем средние коэффициенты эластичности:

С помощью средства Анализ → Основные статистики → Описательные статистики → Итоговая таблица получим основные характеристики переменных:

а) Линейная модель y = a+bx = 1,4272 +1,0504∙x

= b_y_/_x· = 1,0504· 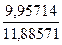= 0,88

б) квадратичная регрессия y = a+bx+cx² = 0,32196+1,32433x–0,01261х²

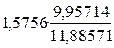= = = = 1,32

в) Экспоненциальная регрессия y = 4,732064·e^0,082605^x

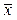= ·b = 9,95714·0,082605 = 0,8225·

г) Степенная регрессия y = 1,6751·e^0,86096^x: = b_y_/_x = 0,86096

д) Гиперболическая регрессия y = 19,7069 –

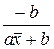= = = = 0,217

10. Рассчитаем для нелинейной модели индекс детерминации.

Индекс детерминации – квадрат коэффициента корреляции, т.е. R². Он характеризует долю дисперсии результативного признака y, объясняемую регрессией, в его общей дисперсии. Индекс детерминации R² выводится в последней строке диалоговом окне «Результаты: …» (как «Объясненная доля дисперсии)».

а) линейная модель y = a+bx: R² = 0,970;

б) квадратическая модель y = a+bx+cx²: R² = 0,972;

в) степенная модель y = ax^b: R² = 0,972;

г) показательная модель y= ae^bx: R² = 0,943;

д) гиперболическая модель y = a+b/x: R² = 0,752.

11. Построим доверительную область для каждой модели.

а) Линейная модель:

Почти все точки лежат внутри доверительной области

б) Квадратичная модель:

Почти все точки лежат внутри доверительной области