Задача №2.
Производится изучение социально-экономических показателей по территориям Сибирского федерального округа РФ за 2000 год..
Y – валовой региональный продукт, млрд. руб.;
X1 – инвестиции 2000 года в основной капитал, млрд. руб.;
X2 – среднегодовая стоимость основных фондов в экономике, млрд. руб.;
X3 – инвестиции 1999 года в основной капитал, млрд. руб.
Требуется изучить влияние указанных факторов на стоимость валового регионального продукта.
Предварительный анализ исходных данных по 12 территориям не выявил территорий с аномальными значениями признаков. Поэтому значения приводимых показателей рассчитаны по полному перечню территорий федерального округа.
При обработке исходных данных получены следующие значения:
А) - линейных коэффициентов парной корреляции, средних и средних квадратических отклонений -σ:
N=12.
| Y | X1 | X2 | X3 | |
| Y | 0,9493 | 0,9541 | 0,9287 | |
| X1 | 0,9493 | 0,9152 | 0,9660 | |
| X2 | 0,9541 | 0,9152 | 0,9582 | |
| X3 | 0,9287 | 0,9152 | 0,9582 | |
| Средняя | 42,43 | 7,758 | 168,6 | 5,208 |
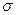
| 36,03 | 6,642 | 114,7 | 3,865 |
Б) - коэффициентов частной корреляции
| Y | X1 | X2 | X3 | |
| Y | 0,7990 | 0,8217 | -0,6465 | |
| X1 | 0,7990 | -0,7054 | 0,8710 | |
| X2 | 0,8217 | -0,7054 | 0,8407 | |
| X3 | -0,6465 | -0,8710 | 0,8407 |
Задание:
1. По значениям линейных коэффициентов парной и частной корреляции выберите неколлинеарные факторы и рассчитайте для них коэффициенты частной корреляции. Проведите окончательный отбор информативных факторов во множественную регрессионную модель.
2. Выполните расчёт бета коэффициентов (b) и постройте с их помощью уравнение множественной регрессии в стандартизованном масштабе. Проанализируйте с помощью бета коэффициентов (b) силу связи каждого фактора с результатом и выявите сильно и слабо влияющие факторы.
3. По значениям b-коэффициентов рассчитайте параметры уравнения в естественной форме (a1, a2 и a0). Проанализируйте их значения. Сравнительную оценку силы связи факторов дайте с помощью общих (средних) коэффициентов эластичности -  .
.
4. Оцените тесноту множественной связи с помощью R и R2, а статистическую значимость уравнения и тесноту выявленной связи - через F-критерий Фишера (для уровня значимости a=0,05).
5. Рассчитайте прогнозное значение результата, предполагая, что прогнозные значения факторов составят 107,7 процента от их среднего уровня.
6. Основные выводы оформите аналитической запиской.