Множественная регрессия.
Значения экономических переменных определяются обычно влиянием не одного, а нескольких объясняющих факторов. Задача оценки статистической взаимосвязи переменных у и х=(х1,х2,…,хm) формулируется аналогично случаю парной регрессии. Ищется функция у=f(a,х)+e, где a– вектор параметров, e– случайная ошибка.
В простейшем случае анализируется линейная зависимость у от х. Уравнение множественной линейной регрессии имеет вид
у=a0+a1х1 +a2х2 +…+amхm+e. (12)
Если имеется n наблюдений факторов х и переменной у, то отклонение зависимой переменной у в j-м наблюдении от линии регрессии
ej= уj – a0 – a1хj1 – a2хj2 – … – amхjm (j=1,2,…, n).
Построение функции (12) проводится в два этапа.
На первом этапе необходимо произвести отбор факторов. Сначала вычисляются коэффициенты корреляции rik по формуле (2) между выборочными значениями факторов Хi={xji} и Хk={xjk}. Если |rik|>0.8 (наблюдается сильная линейная связь между факторами Хi и Хk), то один из них отбрасывается (в принципе, любой, но рекомендуется отбрасывать тот, информацию по которому труднее собрать или она менее достоверна). Затем вычисляются коэффициенты корреляции riу по формуле (2) между выборочными значениями фактора Хi={xji} и Y={yj}. Если |riy|<0.2 (практически отсутствует линейная связь между фактором Хi и анализируемым показателем Y), то и этот фактор отбрасывается.
На втором этапе для оставшихся факторов применяется метод наименьших квадратов. Метод наименьших квадратов предполагает поиск коэффициентов ai таких, что Q=åej2®min. Для отыскания минимума берутся частные производные Q по искомым параметрам (мы использовали этот метод в случае однофакторной регрессии для нахождения a0 и a1) и приравниваются к нулю. После выполнения элементарных преобразований получают так называемую систему нормальных уравнений, из которой и находятся искомые параметры.
Система нормальных уравнений для многофакторной регрессии имеет вид:
 a0 + a1
a0 + a1  1 + a2
1 + a2  2 + … + am
2 + … + am  m =
m = 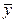 ,
,
a0  1 + a1
1 + a1  + a2
+ a2  + … + am
+ … + am  =
= 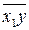 , (13)
, (13)
……………………………………………..
a0 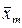 + a1
+ a1  + a2
+ a2  + … + am
+ … + am  =
=  .
.
Для решения системы (13) можно использовать любой метод решения системы линейных уравнений (Гаусса, Крамера и пр.). Оцененное уравнение описывает как общий тренд (тенденцию) изменения зависимой переменной у, так и отклонения от этого тренда. Проблема здесь состоит не только в том, чтобы объяснить возможно большую долю колебаний переменной у, но и отделить влияние каждого из факторов.
 Для анализа статистической значимости полученных коэффициентов множественной линейной регрессии оценивают дисперсию D(ai) и стандартные отклонения S(ai)=ÖD(ai) коэффициентов ai. Аналогично (10) величина t=ai/S(ai), называемая t–статистикой, имеет распределение Стьюдента с (n-m-1) степенями свободы. Если число степеней свободы достаточно велико (не менее 10), то при 5%-ном уровне значимости можно приближенно считать оценку незначимой, если t–статистика по модулю меньше 1, и весьма надежной, если модуль t–статистики больше 3.
Для анализа статистической значимости полученных коэффициентов множественной линейной регрессии оценивают дисперсию D(ai) и стандартные отклонения S(ai)=ÖD(ai) коэффициентов ai. Аналогично (10) величина t=ai/S(ai), называемая t–статистикой, имеет распределение Стьюдента с (n-m-1) степенями свободы. Если число степеней свободы достаточно велико (не менее 10), то при 5%-ном уровне значимости можно приближенно считать оценку незначимой, если t–статистика по модулю меньше 1, и весьма надежной, если модуль t–статистики больше 3.
Коэффициенты множественной линейной регрессии ai имеют большой экономический смысл. Они показывают, на сколько изменится анализируемый показатель Y при изменении фактора Хi на единицу.
Пример 3. Рассмотрим аналитические модели спроса, используя ниже приведенные в табл.3 конкретные статистические данные обследования семей, сведенные в девять групп (с примерно одинаковым объемом потребления).
Таблица 3.
| № группы | Расход на питание (у) | Душевой доход (х1) | Размер семей (х2) | ŷ | ej | ej2 |
| 1,5 | 333,6 | 99,4 | 9880,36 | |||
| 2,1 | 626,5 | –10,5 | 110,25 | |||
| 2,7 | 928,5 | –28,5 | 812,25 | |||
| 3,2 | 1189,8 | –76,8 | 5898,24 | |||
| 3,4 | 1340,5 | –34,5 | 1190,25 | |||
| 3,6 | 1493,6 | –5,6 | 31,36 | |||
| 3,7 | ||||||
| 4,0 | 1879,1 | 34,9 | ||||
| 3,7 | 2409,5 | 1,5 | 2,25 | |||
| Средние | 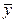 =1313,9 =1313,9
|  1 =6080,5 1 =6080,5
|  2 =3,1 2 =3,1
| 2198,2 |
Рассмотрим сначала однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода (х1)
return false">ссылка скрытаŷ =а0 + а1х1,
параметры которой а0 и а1 находятся по формулам (6), используя данные табл.3 и  =(∑х12)/9=63989644,1,
=(∑х12)/9=63989644,1, 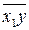 =(∑х1у)/9)=10894351. Решение: а0=660,06; а1 = 0,1075. Получаем уравнение регрессии ŷ =660,06 + 0,1075х1.
=(∑х1у)/9)=10894351. Решение: а0=660,06; а1 = 0,1075. Получаем уравнение регрессии ŷ =660,06 + 0,1075х1.
 Затем вычисляются средняя квадратическая ошибка выборки (корень квадратный из дисперсии у)
Затем вычисляются средняя квадратическая ошибка выборки (корень квадратный из дисперсии у)

 Sу=√(∑(у – у)2)/n,
Sу=√(∑(у – у)2)/n,
 средняя квадратическая ошибка уравнения (4) Sŷ =√(∑(у – ŷ)2)/n и коэффициент детерминации Rŷх1 =√1 – Sŷ2/ Sу2.
средняя квадратическая ошибка уравнения (4) Sŷ =√(∑(у – ŷ)2)/n и коэффициент детерминации Rŷх1 =√1 – Sŷ2/ Sу2.
 В нашем примере Sу2=454070, Sŷ2=63846, следовательно
В нашем примере Sу2=454070, Sŷ2=63846, следовательно
Rŷх1 =√1 – 63846/454070 =0,927.
Полученное значение свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.
Величина R2ŷх1 показывает долю изменения результативного признака под воздействием факторного признака. В нашем примере R2ŷх1 =0,859; это означает, что фактором душевого дохода можно объяснить почти 86% изменения расходов на питание.
Рассмотрим теперь двухфакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода (х1) и размера семьи (х2)
ŷ =а0 + а1х1+ а2х2 .
Параметры модели а0 , а1и а2 находятся посредством решения следующей системы нормальных уравнений:



 а0 + х1а1 + х2а2 = у
а0 + х1а1 + х2а2 = у


 х1а0 +
х1а0 +  а1 + х1х2 а2 = ух1
а1 + х1х2 а2 = ух1


 х2а0 + х1х2 а1 +
х2а0 + х1х2 а1 +  а2 = ух2,
а2 = ух2,

 которая также формируется с применением метода наименьших квадратов (средние величины х1х2 ,
которая также формируется с применением метода наименьших квадратов (средние величины х1х2 ,  и ух2 вычисляются аналогично однофакторной модели). Получаем систему
и ух2 вычисляются аналогично однофакторной модели). Получаем систему
 а0 + 6080,5а1 + 3,1а2 = 1313,9
а0 + 6080,5а1 + 3,1а2 = 1313,9
6080,5а0 + 63989644,1а1 + 21649,1 а2 = 10894351
3,1а0 + 21649,1а1 + 10,2а2 = 4488,
которую решаем, например, методом Гаусса.
Делим второе и третье уравнения на коэффициент при а0.
 а0 + 6080,5а1 + 3,1а2 = 1313,9
а0 + 6080,5а1 + 3,1а2 = 1313,9
а0 + 10523,75а1 + 3,56 а2 = 1791,69
а0 + 6983,58а1 + 3,29а2 = 1447,74.
От второго и третьего уравнения отнимаем первое
 а0 + 6080,5а1 + 3,1а2 = 1313,9
а0 + 6080,5а1 + 3,1а2 = 1313,9
4443,25а1 + 0,46 а2 = 477,79
903,08а1 + 0,19а2 = 133,84.
Делим второе и третье уравнения на коэффициент при а1.
 а0 + 6080,5а1 + 3,1а2 = 1313,9
а0 + 6080,5а1 + 3,1а2 = 1313,9
а1 + 0,0001035 а2 = 0,1075316
а1 + 0,0002104а2 = 0,1482039.
От третьего уравнения отнимаем второе
 а0 + 6080,5а1 + 3,1а2 = 1313,9
а0 + 6080,5а1 + 3,1а2 = 1313,9
а1 + 0,0001035 а2 = 0,1075316
0,0001069а2 = 0,0406723.
Из третьего уравнения находим а2 =380.47; подставляя его во второе уравнение получаем а1 = 0,06815; подставляя найденные а1и а2 в первое уравнение, получаем а0 = –279.94; следовательно
ŷ = –279.94 + 0.06815х1+ 380.47х2 .
Для определения тесноты связи предварительно вычисляются теоретические значения ŷ, затем уклонения ej и их квадраты (колонки 5,6,7 табл.3). Получим Sŷ2 =(∑(у – ŷ)2)/n =2198,2. Используя ранее вычисленное Sу2=454070, получим R2 =1 – Sŷ2/ Sу2 =0,995. R2 показывает долю вариации результативного признака под воздействием изучаемых факторных признаков. У нас R2=0,995; это означает, что совместное влияние душевого дохода и размера семей объясняет почти 99,5% изменения расходов на питание.
Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае линейной двухфакторной модели рассчитываются по формулам



 Э ŷх1(х2) = а1х1 / у; Э ŷх2(х1)= а2х2 / у. (14)
Э ŷх1(х2) = а1х1 / у; Э ŷх2(х1)= а2х2 / у. (14)
Частные коэффициенты эластичности показывают, на сколько процентов изменится результативный признак, если изменить один из факторных признаков на один процент не меняя значения остальных.
В рассматриваемом выше примере 3 Эŷх1(х2)=0,06815·6080,5/1313,9=0,315; Эŷх2(х1)=380.47·3,1/1313,9=0,898. Это означает, что при увеличении душевого дохода на один процент и неизменном размере семьи расходы на питание увеличатся на 0,315 процента, а увеличение на один процент (условно) размера семьи при неизменном душевом доходе приведет к росту расходов на питание на 0,898 процента.
Пример 4. Как размер платы за квартиру зависит от площади квартиры и от количества человек, прописанных в данной квартире.
Данные приведены в табл. 4.
Таблица 4
| N | Квартплата, руб. | Площадь квартиры, м2 | Количество человек |
| y | x1 | x2 | |
| 244,19 | 46,0 | ||
| 450,50 | 80,2 | ||
| 199,86 | 43,8 | ||
| 192,00 | 48,9 | ||
| 98,50 | 12,0 | ||
| 356,59 | 59,8 | ||
| 381,54 | 51,9 | ||
| 118,48 | 18,0 | ||
| 324,40 | 53,8 | ||
| 182,50 | 16,0 | ||
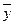 =254,86 =254,86
|  1=43,04 1=43,04
|  2=2,5 2=2,5
|
Построим линейную аддитивную модель в виде ŷ=а0+а1x1+а2x2. Необходимые данные для расчета модели сведем в табл. 5.
Таблица 5
| N | yx1 | yx2 | x12 | x22 | x1x2 |
| 11232,74 | 732,57 | ||||
| 36130,1 | 1351,5 | 6432,04 | 240,6 | ||
| 8753,87 | 199,86 | 1918,44 | 43,8 | ||
| 9388,8 | 2391,21 | 97,8 | |||
| 98,5 | 12,0 | ||||
| 21324,08 | 1069,77 | 3576,04 | 179,4 | ||
| 19801,93 | 1526,16 | 2693,01 | 207,6 | ||
| 2132,64 | 236,96 | ||||
| 17452,72 | 973,2 | 2894,44 | 161,4 | ||
| 547,5 | 48,0 | ||||

|  1=13031,9 1=13031,9
|  2=712 2=712
|  =2274,58 =2274,58
|  =7,1 =7,1
| х1х 2=116,46 |
Для решения линейной двухфакторной модели строим следующую систему уравнений:
 а0+
а0+  1a1+
1a1+  2a2 =
2a2 = 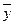

 1а0+
1а0+  a1+ х1х 2a2 =
a1+ х1х 2a2 =  1
1

 2а0+ х1х 2a1+
2а0+ х1х 2a1+  a2 =
a2 =  2.
2.
Нам нужно решить систему из трех линейных уравнений с тремя неизвестными и найти значения коэффициентов модели а0, а1 и а2.
 Подставляя в данную систему найденные числовые данные, получим систему
Подставляя в данную систему найденные числовые данные, получим систему
а0+43,04 a1+2,5 a2 = 254,86
43,04 а0+2274,58 a1+116,46 a2 = 13031,89
2,5 а0+116,46 a1+7,1 a2 = 712.
Для того чтобы решить данную систему уравнений методом Крамера, найдем сначала значение определителя основной матрицы. Этот определитель определяется равенством
| ∆ = | 43,04 2,5 | 43,04 2274,58 116,46 | 2,5 116,46 7,1 | = 1 | 2274,58 116,46 | 116,46 7,1 | - 43,04 | 43,04 2,5 | 116,46 7,1 |
| + 2,5 | 43,04 2,5 | 2274,58 116,46 | =1×(16149,518-13562,93)-43,04×(305,58-291,1)+2,5× |
×(5012,44–5686,45)=2586,586 – 621,07 – 1685,025=280,49.
Получили, что ∆=280,49≠0, значит, система уравнений имеет единственное решение, которое находится по формулам Крамера
∆а0 ∆а1 ∆а2


 а0 = , а1 = , а2 = .
а0 = , а1 = , а2 = .
∆ ∆ ∆
| ∆а0 = | 254,86 13031,89 | 43,04 2274,58 116,46 | 2,5 116,46 7,1 | = 254,86 | 2274,58 116,46 | 116,46 7,1 | – 43,04× |
| 13031,89 | 116,46 7,1 | + 2,5 | 13031,89 | 2274,58 116,46 | = 254,86×(16149,52-13562,93)- |
- 43,04×(92526,42–82919,52) + 2,5×(1517693,9–1619500,96) = 659218,33 –
– 413480,98–254515,25= –8777,9.
| ∆а1= | 43,04 2,5 | 254,86 13031,89 | 2,5 116,46 7,1 | =1 | 13031,89 | 116,46 7,1 | – 254,86 | 43,04 2,5 | 116,46 7,1 |
| + 2,5 | 43,04 2,5 | 13031,89 | =1×(92526,42–82919,52)–254,86×(305,58–291,15)+2,5× |
×(30644,48–32579,72)=9606,9–3677,63–4838,1=1091,2.
| ∆а2= | 43,04 2,5 | 43,04 2274,58 116,46 | 254,86 13031,89 | = 1 | 2274,58 116,46 | 13031,89 | – 43,04× |
| 43,04 2,5 | 13031,89 | + 254,86 | 43,04 2,5 | 2274,58 116,46 | = 1×(1619500,96–1517693,91) – |
– 43,04 ×(30644,48 – 32579,73) + 254,86 × (5012,44 –5686,45) =
=101807,05+83293,16–171778,19=13322,02.
Теперь мы можем найти значения коэффициентов модели а0, а1 и а2.
а0 = –8777,9/280,49= –31,3;
а1 = 1091,2/280,49= 3,89;
а2 = 13322,02/280,49= 47,5,
следовательно, линейная аддитивная модель имеет следующий вид:
ŷ= –31,3+3,89 x1+47,5 x2.
Коэффициент регрессии модели а1 =3,89 показывает, что каждый метр площади квартиры повышает квартплату на 3,89 руб., а коэффициент а2=47,5 показывает, что каждый прописанный человек повышает квартплату на 47,5 руб.
Найдем теоретические значения ŷ и их отклонения от априорных (данные приведены в табл.6).
Таблица 6.
| номер | y | (y - 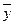 )2 )2
| ŷ | ε=ŷ - у | ε2 |
| 244,19 | 113,85 | 290,14 | 45,9 | 2106,8 | |
| 450,50 | 38275,01 | 423,1 | –27,4 | 750,8 | |
| 199,86 | 186,52 | –13,3 | 176,9 | ||
| 192,00 | 3951,38 | 253,88 | 61,9 | 3831,6 | |
| 98,50 | 24448,45 | 62,88 | –35,6 | 1267,4 | |
| 356,59 | 10348,99 | 343,79 | –12,8 | 163,8 | |
| 381,54 | 16047,82 | 360,61 | –20,9 | 436,8 | |
| 118,48 | 18599,50 | 133,74 | 15,3 | 234,1 | |
| 324,40 | 4835,81 | 320,47 | –3,9 | 15,2 | |
| 182,50 | 5235,97 | 173,5 | –9 | ||
| ∑/n | 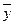 =254,86 =254,86
| 12488,18 | 906,4 |
Совокупный коэффициент детерминации
R2 = 1 – 906,4/12488,18= 0,927.
Значение данного коэффициента близко к 1, что очень хорошо.
2.5. Формирование регрессионных моделей на компьютере с помощьюППП Excel