Е) Модели Бокса-Дженкинса для нестационарных рядов

Модели Бокса-Дженкинса могут применяться и для описания нестационарных рядов, которые путем взятия разностей приводятся к стационарным. Например, стационарным может оказаться процесс

 

 

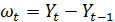
Для таких процессов модель Бокса-Дженкинса представляется в виде

 

(4. 8.17)

 

где ;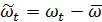

− стационарный процесс, образованный d-й разностью процесса ;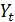

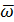– среднее значение процесса ;

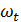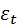− некоррелированная случайная величина с нулевым математическим ожиданием;

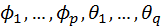− параметры модели (авторегрессии и скользящего среднего).

Прогнозирование показателей на основе моделей Бокса-Дженкинса включает следующие этапы:

– идентификацию типа модели (определение порядка взятия разности d, числа членов авторегрессии p и скользящего среднего q);

– предварительную оценку параметров модели;

– уточненную оценку параметров модели;

– диагностическую проверку ее адекватности;

– использование модели для прогнозирования, расчет дисперсии ошибок прогноза.

На первом этапе последовательно производится взятие очередной

(d-й) разности исходного временного ряда

 

w_t= D^d = (1-B)^d , (4. 8.18)

 

где B − оператор сдвига назад (B = );

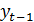D − оператор взятия разности (D = - ).

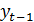Выбор порядка разности d осуществляется последовательным перебором d=0,1,... до получения минимума дисперсии разностного временного ряда.

Для полученного разностного ряда вычисляются оценки:

– среднего значения

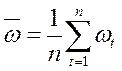, (4.8.19)

где n = N – d;

N − число точек исходного временного ряда;

– автоковариационной функции

 

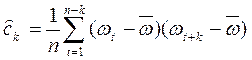(k = 0,…, n/3); (4. 8.20)

 

– автокорреляционной функции

(k = 0,…, n/3 ); (4.8.21)

 

– частной автокорреляционной функции

 

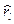при l=1

=

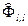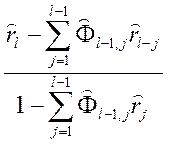(l=2,…, n/3), (4.8.22)

где 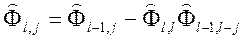( j = 1,…, l-1 ).

Дальнейшая идентификация типа модели (определение параметров p и q) осуществляется на основании анализа поведения автокорреляционной и частной автокорреляционной функций. У процесса авторегрессии порядка p - АР(p) частная автокорреляционная функция равна нулю при k > p, а у процесса скользящего среднего порядка q - СС(q) автокорреляционная функция равна нулю при k > q.

Формула для оценки дисперсии выборочного коэффициента автокорреляции при задержках k, больших q, за которыми автокорреляционная функция процесса СС(q) равна нулю, получена Bartlett M. S. и имеет вид

 

. (4. 8.23)

Этот результат может использоваться для определения числа членов скользящего среднего q путем статистической проверки гипотезы

 

Н₀: r_k=0 (k > q).

 

Гипотеза не отвергается, если

 

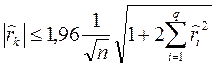(k > q) . (4. 8.24)

 

Отметим, что в формуле (4. 8.24) вместо истинных значений r_iстоят их оценки .

Если q невелико ( q £ 2 ), то процесс можно описать в виде модели скользящего среднего СС(q).

Определяется число членов авторегрессии - p из условия, что при k > p случайная величина 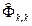имеет нормальное распределение с нулевым математическим ожиданием и дисперсией D ( 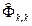) » 1 / n . Этот факт можно использовать для статистической проверки гипотезы о равенстве нулю истинных значений Ф_k,k для k > p.

Гипотеза не отвергается, если

 

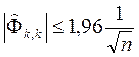(k > p) . (4. 8.25)

Если p невелико ( p £ 2 ), то процесс можно описать в виде модели авторегрессии АР( p ).

Из величин p и q выбирается наименьшее, и процесс полагается либо СС(q), либо АР(p). Если p=q или p и q достаточно велики, то процесс следует идентифицировать как смешанный процесс АРСС(1,1).

Для решения вопроса идентификации моделей можно использовать ряд критериев:

– информационный критерий Акаике

 

ИКА (p;q) = n ln S²(p;q) + 2 (p+q);

– байесовский информационный критерий

 

БИК (p;q) = ln S²(p;q) + (p+q) ln n / n;

 

– критерий Хеннана-Куина

 

XK (p;q) = ln S²(p;q) + (p+q) c ln( ln n / n).

 

Здесь S²(p;q) − оценка дисперсии s²остаточного ряда, а с − некоторая константа (c > 2) .

Процедура подгонки состоит в вычислении критериальной функции для различных значений p и q и выборе тех p и q, при которых величина критериальной функции минимальна.

На втором этапе осуществляется предварительная оценка параметров авторегрессии и скользящего среднего.

Рассмотрим сначала процесс авторегрессии АР(р).

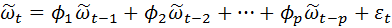(4.8.26)

 

Умножим (4.8.26) на :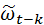

Берем математическое ожидание и получаем разностное уравнение для автоковариации μ( )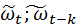

 

 

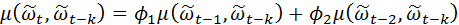
Отметим, что 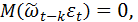когда k>0, так как 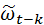может включать реализации ε, имевшие место до момента t-k, а они некоррелированы с 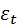. Разделив все члены на дисперсию процесса, получим разностное уравнение для автокорреляционной функции

 

(4.8.27)

 

Имея коэффициенты автокорреляции, можно с их помощью оценить параметры авторегрессии. Для этого подставим в (4.8.27) k=1,2,..,p и получимсистему линейных уравнений для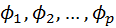

 

………………………………………………

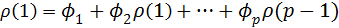
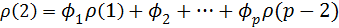
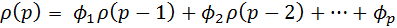
(4.8.28)

Система уравнений (4.8.28) называется системой уравнений Юла – Уокера. Заменив теоретические автокорреляции на их оценки 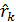, можно получить оценки параметров модели авторегрессии.

Для модели скользящего среднего первоначальная оценка параметров может осуществляться на основе следующих соотношений

 

(4.8.29)

Задавая k=1,2,..,q , получим систему уравнений, которая является нелинейной относительно оцениваемых параметров 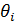и решается с помощью итеративных процедур.

Таким образом, оценка параметров авторегрессии Ф (если р >0) находится из системы p линейных уравнений Юла-Уокера, а оценка параметров скользящего среднего Q осуществляется с помощью сложной итеративной процедуры.

На третьем этапе осуществляется уточнение оценок 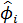и 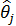, полученных на предыдущем этапе, с помощью алгоритма Марквардта, цель которого заключается в минимизации суммы квадратов e_tпо параметрам 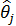и .

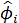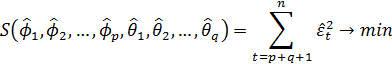
Диагностическая проверка адекватности моделей сводится к проверке статистической гипотезы о некоррелированности случайных величин e_t. Для этого могут использоваться критерий Дарбина-Уотсона и совокупный критерий согласия Бокса-Пирса. Этот вопрос будет рассмотрен несколько позже.

На последнем этапе производится вычисление прогнозных значений показателя. Для этого модель

 

Ф(B) ( 1 - B )^d 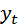= Q(B) e_t (4.8.30)

 

приводится к виду

 

,

(4.8.31)

где величины 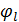получаются как коэффициенты при B^lв произведении

( 1 - B )^d на Ф(B).

Формула (4.8.31) позволяет прогнозировать y_t рекуррентно для t=t+1, t+2, ...., t+L , где t − текущий момент времени. При этом на i-м шаге в качестве величин y_t+1, y_t+2, ... y_t+i-1 используются их прогнозы, полученные на предыдущих шагах − 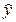_t+1, 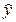_t+2, ... 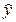_t+i-1, а e_t+1, e_t+2, ... e_t+i-1 полагаются равными нулю. Величины ε_t, e_t-1, e_t-2, ... e_t-q определяются на этапе уточненной оценки параметров модели.

Дисперсия ошибок прогноза вычисляется по формуле

 

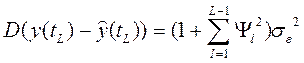, (4.8.32)

где - дисперсия ,

а величины y_lопределяются по формулам

y₀= 1

y₁= j₁- q₁

y₂= j₁y₁+ j₁- q₂

..................................

y_l= j₁y_l-1+ .... + j_p+dy_l-p-d- q_l.

 

При этом q_l = 0 для l > q и y_l = 0 при l < 0 .

 

4.9. МОДЕЛЬ С ЦИКЛИЧНОСТЬЮ РАЗВИТИЯ

Наиболее распространенный подход к построению математических моделей прогнозирования циклических процессов заключается в первоначальном выделении тренда и анализе остаточного ряда в целях выявления и описания периодической компоненты. Для выделения тренда можно использовать процедуру сглаживания временных рядов с помощью метода скользящего среднего.

При анализе сезонных колебаний задача упрощается за счет того, что мы знаем их период – 1 год (это относится и к другим циклическим процессам с постоянным и известным периодом).

Скользящая средняя, применяемая для этой цели, должна иметь строго определенный период скольжения – 12 месяцев или 4 квартала. При этом индекс сезонности можно определить как отношение фактического уровня ряда к уровню, рассчитанному по скользящей средней. Очевидно, что значения индекса сезонности для данного месяца (квартала) будут различаться из года в год. Поэтому в качестве индекса сезонности следует использовать среднее значение индексов, полученных за ряд лет по одноименным месяцам или кварталам.

Однако полученные при этом данные относятся к интервалам с серединами между кварталами, а не к серединам интервалов (15 февраля, 15 мая, 15 августа, 15 ноября). Поэтому необходимо «центрировать» среднее. Наиболее просто это можно сделать, взяв средние последовательных пар средних, вычисленных по 4-м элементам. Такой процесс эквивалентен вычислению средних пяти элементов с весами [ ].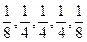

Если средний индекс сезонности за 12 месяцев или 4 квартала не равен единице, производится выравнивание индексов сезонности – деление всех индексов на их средний индекс.

Отметим, что разумно считать, что влияние сезонности носит мультипликативный характер. В этом случае

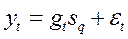, (t=1,…,n ; q=1,…,4) (4.9.1)

где s_q – индекс сезонности;

g_t – трендовая составляющая временного ряда.