Найдем ковариационную матрицу оценок
.
В этой матрице элементами главной диагонали являются дисперсии оценок 
.
Выполним преобразование
,
откуда 
.
Тогда
.
Полученное выражение содержит матрицу 
M(eeT) = 
В данной матрице все элементы, не лежащие на главной диагонали, равны 0 (в силу предположения о некоррелированности ошибок ei). Поскольку все ошибки имеют одинаковую дисперсию, то
,
где Е – единичная матрица.
Окончательно получим
. (4.6.4)
Так как величина s2 неизвестна, в качестве ее оценки используется величина
. (4.6.5)
Определим теперь дисперсию ошибки прогноза. Если tL – прогнозный момент времени, то прогноз по полиномиальной модели имеет вид
.
Отметим, что
,
т. е. мы получили несмещенный прогноз среднего уровня 
+ 
+ 
Это выражение можно записать в матричной форме
,
где TTL= ( 1 tL tL2 …… tLm ).
Учитывая (4.6.4), получим
.
Поскольку s2 неизвестна, будем использовать ее оценку
.
Ошибка прогноза обусловлена не только ошибкой оценки среднего, но и случайным отклонением от среднего уровня
,
где – истинное значение среднего уровня.
Тогда
= 
.
Окончательно
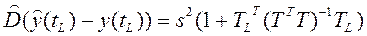. (4.6.6)
ПРИМЕР. Динамика объема продаж некоторого товара (тыс.шт.) за 9 лет приведена в табл. 4.3.
Таблица 4.3.
| Год | ti | yi | tiyi | ti2 | yiti2 | ti3 | ti4 |  (t)
|
| 18,2 | 18,2 | 18,2 | 17,6 | |||||
| 20,1 | 40,2 | 80,4 | 20,9 | |||||
| 23,4 | 70,2 | 210,6 | 23,3 | |||||
| 24,6 | 98,4 | 393,6 | 24,1 | |||||
| 25,6 | 128,0 | 640,0 | 25,5 | |||||
| 25,9 | 155,4 | 932,4 | 25,3 | |||||
| 23,6 | 165,2 | 1156,4 | 24,2 | |||||
| 22,7 | 181,6 | 1452,8 | 22,3 | |||||
| 19,2 | 172,8 | 1555,2 | 19,4 | |||||
| Cумма | 203,3 | 1030,0 | 6439,6 | 203,3 |
Из таблицы видно, что в течение первых 6 лет объем продаж товара возрастал, а в последние 3 года снижался. Это говорит о невозможности аппроксимации временного ряда линейной зависимостью.
Попробуем описать динамику полиномом 2-го порядка (параболой)
.
Система уравнений для оценки параметров полинома 2-го порядка имеет вид:
,
,
.
Для нашего примера (см. итоговую строку таблицы):
,
,
.
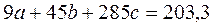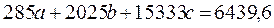Решение этой системы дает коэффициенты полинома
,
а математическая модель принимает вид
.
Полученные с ее помощью «прогнозы» (для t=1,…,9) приведены в последнем столбце таблицы. Нетрудно заметить, что они достаточно близки к реальным данным.
4.7. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ. АВТОКОРРЕЛЯЦИОННАЯ ФУНКЦИЯ.
Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени.
Случайным процессом Y(t) называется функция от t,которая при любом значении t является случайной величиной.
Временной ряд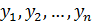 
можно рассматривать как одну из реализаций (траекторий) случайного процесса Y(t).
Временной ряд 
называется строго стационарным (или стационарным в узком смысле), если совместное распределение вероятностей случайных величин
точно такое же, как и для случайных величин
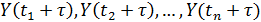
для любых t,τ и n.
Для стационарных временных рядов определяют степень тесноты связи между Y(t) и 
ибо
,
.
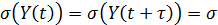Зависимость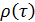 
называют автокорреляционной функцией. В силу стационарности временного ряда автокорреляционная функция зависит только от лага τ.
Под стационарным процессом в широком смысле понимают случайный процесс, у которого среднее и дисперсия не зависят от t, а автокорреляционная функция зависит только от длины лага между рассматриваемыми переменными
,
,
,
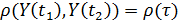где 
Основная проблема в оценивании параметров случайного процесса состоит в том, что фактически имеется только одна его реализация. Данную проблему можно решить с использованием понятия эргодичности – замены усреднения по множеству реализаций случайного процесса усреднением по времени. Эргодичность делает возможным оценивание 
только по одной его реализации – временному ряду.
Оценка математического ожидания
= 
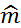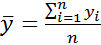
Оценка дисперсии
Оценка автокорреляции (выборочный коэффициент автокорреляции 
)
= 
Функцию называют выборочной корреляционной функцией, а ее график – коррелограммой. При расчете 
следует помнить, что с увеличением τ число n-τ пар наблюдений 
уменьшается, поэтому лаг 
должен быть таким, чтобы число n-τ было достаточным для определения . Обычно 
.
4.8. АДАПТИВНЫЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ
При прогнозировании стационарных процессов используются так называемые адаптивные модели, к числу которых относятся модели экспоненциального сглаживания и модель Бокса-Дженкинса, которая является более общей по отношению к модели экспоненциального сглаживания.