Проверка значимости уравнения регрессии

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.

В математической статистике дисперсионный анализ рассмотрен как самостоятельный метод статистического анализа. Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели.

Обозначим Согласно основной идее дисперсионного анализа

(2.5.24)

или

(2.5.25)

где Q – общая сумма квадратов отклонений зависимой переменной от средней, а Q_R и Q_e - соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов.

Убедимся в том, что пропущенное в (2.5.25) третье слагаемое равно 0. Учитывая (2.5.17), (2.5.11), имеем:

Теперь

(с учетом соотношения (2.5.10).

Схема дисперсионного анализа имеет вид, представленный в таблице.

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Средние квадраты
Регрессия		m-1
Остаточная		n-m
Общая		n-1

Средние квадраты и представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной Х ивоздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров уравнения регрессии; n – число наблюдений.

При отсутствии линейной зависимости между зависимой и объясняющими переменными случайные величины и имеют - распределение соответственно с m-1 и n-m степенями свободы, а их отношение – F- распределение с теми же степенями свободы. Поэтому уравнение регрессии значимо на уровне 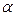, если фактически наблюдаемое значение статистики

, (2.5.26)

где - табличное значение критерия Фишера, определенное на уровне значимости 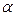при k₁=m-1 и k₂=n-m степенях свободы.

В случае линейной парной регрессии m=2, и уравнение регрессии значимо на уровне 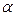, если

(2.5.27)

Мерой качества регрессионной модели, характеристикой прогностической силы регрессионной модели является коэффициент детерминации, определяемый по формуле

(2.5.28)

Величина R² показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.

Так как , то .

Чем ближе к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линейной регрессии. Если =1, то эмпирические точки (x_i,y_i) лежат на линии регрессии и между переменными Y и X существует линейная функциональная зависимость. Если =0, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.

Средняя ошибка аппроксимации

Еще одним показателем качества построенной регрессионной зависимости является средняя ошибка аппроксимации, которая вычисляется по формуле

Эта величина представляет собой среднюю относительную ошибку.

Пример

Исследуем зависимость розничного товарооборота магазинов (млрд р.) от среднесписочного числа работников. Обозначим:

x – число работников;

y – товарооборот.

Исходные данные и результаты расчетов приведены в таблице

Номер магазина

0,5 39,5 6 241 0,25

0,7 59,5 7 225 0,49

0,9 91,8 10 404 0,81

1,1 126,5 13 225 1,21

1,4 170,8 14 884 1,96

1,4 176,4 15 876 1,96

1,7 227,8 17 956 2,89

1,9 279,3 21 609 3,61

Итого 9,6 1171,6 107 420 13,18

;

; ;

;

Вычислим выборочный коэффициент корреляции:

;

;

.

Тогда

Проверим значимость выборочного коэффициента корреляции. Для этого вычислим статистику t:

Табличное значение критерия Стьюдента для = n-2 = 6 и

Так как 15,65 > 2,45 , то полученный коэффициент корреляции статистически значим.

Найдем коэффициенты парной линейной регрессии:

;

и регрессия имеет вид

.

Прогнозное значение розничного товарооборота при составит

2.6. МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной Y от нескольких объясняющих переменных X₁, X₂, …, X_k. Эта задача решается с помощью множественного регрессионного анализа.

Модель множественной линейной регрессии имеет вид

; (2.6.1)

или

;

(i=1,…,n) (2.6.1 а)

Модель (2.6.1), в которой зависимая переменная 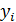, возмущения и объясняющие переменные ,…, удовлетворяют приведенным выше предпосылкам 1-5 регрессионного анализа, называется классической нормальной линейной моделью множественной регрессии.

Включение в регрессионную модель новых объясняющих переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности использования матричных обозначений.

Введем обозначения

– вектор-столбец значений зависимой переменной размера n;

Х=

- матрица значений объясняющих переменных размера n(k+1).

где x_ij – значение j-ой переменной для i-го объекта выборки.

Обращаем внимание на то, что в матрицу Х дополнительно введен столбец, все элементы которого равны 1, т. е. условно полагается, что в модели (2.6.1) свободный член умножается на фиктивную переменную , принимающую значение 1 для всех i: ;

– вектор-столбец параметров размером k+1;

- вектор-столбец возмущений (случайных ошибок, остатков) размера n.

Тогда в матричном виде модель (2.6.1) примет вид

(2.6.2)

Как уже было отмечено, модель (2.6.2), удовлетворяющая приведенным предпосылкам 1-5, называется классической нормальной линейной моделью множественной регрессии. Если же среди приведенных предпосылок не выполняется лишь предпосылка 5 о нормальном законе распределения вектора возмущений ε, то модель (2.6.2) называется просто классической линейной моделью множественной регрессии.

Оценки параметров а₀, a₁, … a_k можно получить с помощью рассмотренного ранее метода наименьших квадратов.

Система уравнений имеет вид

,

,

……..

.

Суммирование производится по индексу i от 1 до n, где n –объем выборки.

Эту систему обычно записывают в матричном виде

,

где - транспонированная матрица;

Умножив обе части уравнения слева на матрицу ,