Решение.
1) Построение поля корреляции:

| у | |||||||||||||||||||||||

| х |
2) Построение и анализ линейной модели регрессии:
Для расчета параметров a и b линейной регрессии y = a + b x, в соответствии с методом наименьших квадратов,необходимо решить систему нормальных уравнений относительно a и b:

Из этой системы получаются следующие формулы:
b=  ; (1)
; (1)
а=  (2)
(2)
По исходным данным рассчитываем S y, S x, S y x, S x2, S у2. Для удобства результаты вычислений заносим в таблицу 1:
Таблица 1
| i | yi | xi | yi xi | xi2 | yi2 | yxi | y - yxi | Ai |
| Сумма | ||||||||
| Среднее значение | * | * |
Подставляя полученные средние значения в формулы (1)и (2), находим
b=
а=
Получили следующее уравнение линейной регрессии: y = ___ ____ ∙x.
Из уравнения следует, что с увеличением заработной платы на 1 у.е. доля расходов на ________________________ в среднем на ___ % - ных пункта.
3) Для оценки тесноты связи изучаемых явлений рассчитаем линейный коэффициент парной корреляции:
rxy = 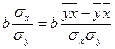 =
=
Полученное значение rxy показывает, что связь ______________________________________.
4)
а) Определим коэффициент детерминации R2, который характеризует долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака:
R2 =rxy2=
Значение R2 указывает на то, что вариация результативного признака у на _______ % объясняется вариацией признак - фактора х.
б). Оценку качества полученного уравнения регрессии дает также средняя ошибка аппроксимации Ā.
Для того, чтобы вычислить Ā, произведем следующие расчеты:
подставим в уравнение регрессии фактические значения х и определим теоретические (расчетные) значения ŷх (заполняем 7-ой столбец таблицы 1);
найдем разности y - ŷxi (8-ой столбец таблицы 1) и величины Аi=  %(9-й столбец таблицы 1).
%(9-й столбец таблицы 1).
Теперь находим
Ā = Σ Ai/n =
Как видим, в среднем расчетные значения отклоняются от фактических на __________%, что
_______________________________________________________________________________.
в) Оценим качество уравнения регрессии с помощью F-теста. F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы.
Рассчитаем фактическое значение F-критерия Фишера:
 Fфакт =
Fфакт = 
Здесь n – число единиц совокупности; m – число параметров при переменных х.
В данной задаче получили FтаблFфакт , что указывает на необходимость принять (отвергнуть) гипотезу Н0 о случайной природе выявленной зависимости и статистической незначимости параметров уравнения регрессии и показателя тесноты связи.