Пример проведения расчетов в Excel
| Год | Y | C | I | G | Y^ | C^ | I^ | G^ | ΔC2 | ΔI2 | ΔG2 |
| 6,3 | |||||||||||
| 13,7 | |||||||||||
| …. | |||||||||||
| 59,51 | -65,77 | -29,08 | |||||||||
| …. | |||||||||||
| ΣΔC2 | ΣΔI2 | ΣΔG2 |
Попробуем настроить, исследовать и модифицировать модель Самуэльсона–Хикса и одну из версий модели Кейнса.
Экономическим объектом служит закрытая экономика. Ее состояние в текущем периоде t описывается переменными (Yt, Ct, It, Gt). Концептуальная модель Самуэльсона-Хикса:
1) Текущее потребление объясняется уровнем ВВП в предыдущем периоде, возрастая вместе с ним, но с меньшей скоростью;
2) Величина инвестиций прямо пропорциональна приросту ВВП за предшествующий период (прирост ВВП за предшествующий период – это разность Yt-1 – Yt-2);
3) Государственные расходы возрастают с постоянным темпом роста;
4) текущее значение ВВП есть сумма текущих уровней потребления, инвестиций и государственных расходов (тождество системы национальных счетов).
В сокращённом виде:
Потребление = a0 + a1 * ВВП(t-1)
Инвестиции = b * ( ВВП(t-1) – ВВП(t-2)) = b * (рост ВВП в прошлом году)
Госрасходы = g * Госрасходы (t-1)
ВВП = Потребление + Инвестиции + Госрасходы
Модели Самуэльсона-Хикса (слева) и Кейнса (справа) похожи, но значения C и I вычисляются с использованием разных Y.
| C = a0 + a1Y t-1 I = b0 + b1(Y t-1 – Y t-2) G = gG t-1 Y = C + I + G 0 < a1 < 1, b > 0, g > 0 | C = a0 + a1Y t +a2Y t-1 I = b0 + b1Y t + b2Y t-1 Y = C+ I + G |
Особую сложность представляет построение уравнения для инвестиций I, так как их значения не аппроксимируются гладкой функцией и их колебания коррелируют с (Yt-1 – Yt-2), что видно на Рисунке 9.1, на котором также представлены оцененные значения I^ :
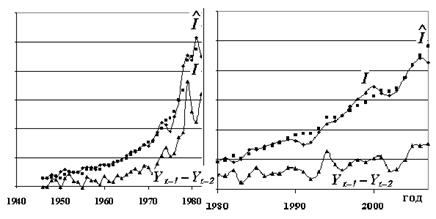 |
Рис. 9.1. Зависимость Iи I^ от Yt-1 –Yt-2.
Модель Самуэльсона–Хикса в исходном виде подогнать не удалось, т.к. прямая пропорциональность I разности Y привела к большим колебаниям I^. Инвестиции вычислялись по формуле, аналогичной модели Кейнса, но со сдвигом Y назад на 1 год:
I = b0 + b1Yt-1 + b2Yt-2
Государственные расходы G также не удалось аппроксимировать по исходной формуле, в уравнение была добавлена константа g0. Расчет коэффициентов для оценки G проводился отдельно. Использован Сервис “Поиск решения” Excel, целевая ячейка ΣΔG2,т.е.сумма квадратов отклонений истинных и расчетных значений за период 1946-2002 г.г., изменяемые значения – коэффициенты g0 и g. При расчете коэффициентов для C и I целевая ячейка (ΣΔC2 + ΣΔI2). В результате получена модифицированная модель Самуэльсона–Хикса:
R2 прогноза
C = -28,9 + 0,721Y t-10,86
I = -10,34 + 0,424Y t-1 - 0,268Y t-2 0,71
G = 3,85 + 1,057G t-1 0,995
Y = C + I + G 0,84
и модель Кейнса:
C = -35,67 +0,157Y t + 0,556Y t-1 0,67
I = -16,9 + 0,3535Y t - 0,202 Y t-1 0,74
Y = C+ I + G 0,74
Точность и адекватность моделей оценена по индексам детерминации
R2 = 1 – Σост2 /TSS ,
где TSS =Σ (Х – Хсредн.)2 , X = Y, C, I, G. В диапазоне настройки R2 > 0,99 ; в диапазоне прогноза (2003-07 г.г.) индексы детерминации для моделей Самуэльсона–Хикса и Кейнса представлены выше рядом с формулами. Точность прогноза нельзя назвать хорошей, и завышенные прогнозы Y и C видны на Рисунке 9.2. Возможно, это связано со спадом темпа роста инвестиций в 2002-03 г.г., что видно на Рисунке 1 и с уменьшением темпов роста всех показателей с начала 80-х.
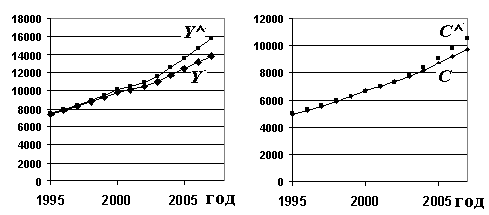 |
Рис.9.2. Реальные и прогнозные значения ВВП (Y) и потребления (C) по модели Самуэльсона–Хикса.
Мы опробовали также настройку моделей, существенно отличающихся от классических, в которых функции Y, C, I, G близки к экспонентам, за исключением пилообразных отклонений I. Мы провели линеаризацию этих функций логарифмированием, а затем строили модели. Графики натуральных логарифмов Y, C, G, I представлены на Рисунке 9.3.
 |
Рис. 9.3. Графики натуральных логарифмов Y, C, G, I
Были опробованы несколько моделей. Наиболее точные прогнозы на 2003-07 г.г. получены по следующей модели:
R2 прогноза
ln C^ = – 0,429 + 1,0096 ln Yt 0,987
ln I^ = –1,60 +ln (2,167 Yt – 1,502 Yt-1) 0,945
ln G^ = – 1,13 + 0,946 Y t-1 0,925
ln Y^ = ln (C^ + I^ +G^) 0,986
Графики реальных и прогнозных величин в 2003-07 г.г. практически совпали.
Как видим, регрессия по ВВП и его приросту дает хорошие результаты. А как спрогнозировать ВВП? Линейная регрессия ВВП по времени дала волнообразный график остатков, представленный на Рисунке 9.4А. Его период совпал с периодом циклов Кондратьева – примерно 40 лет. Поэтому была проведена аппроксимация зависимости ВВП от времени функцией
Y(t) = a + bt + d Sin(ωt + φ).
Настройка этой модели проведена с помощью сервиса “Поиск решения” Excel, изменяемые ячейки – пять коэффициентов a, b, d, ω, φ. Остатки стали случайными (Рис. 9.4В), кроме последнего участка, где реальный ВВП на самом деле несколько упал.
 |
Рис. 9.4. Разности логарифмов реального и оцененного ВВП при линейной (А)
и линейно-синусоидальной (В) регрессии.
ВЫВОД: В целом, применение итерационных градиентных методов, заложенного в сервис “Поиск решения” Excel, позволяет достаточно просто, быстро и наглядно настраивать и исследовать системы одновременных уравнений, описывающие экономические процессы. Точность аппроксимации в диапазоне настройки получается весьма высокой, даже при колебаниях переменных. Остается открытым вопрос об устойчивости решений и о надежности прогноза, особенно при колебаниях переменных в конце диапазона настройки.
Исследуйте модель, увеличив обучающую выборку, а также используя дополнительные статистические данные по экономикам разных стабильных стран. Исследуйте аналогичным образом другие макроэкономические модели. В принципе, таким образом можно сделать дипломную работу или даже кандидатскую диссертацию, но следует быть очень осторожным: поисковые работы в этих случаях опасны, можно ожидать критики в связи с недостаточным теоретическим обоснованием применяемых технологий.
Контрольные вопросы