Единицы длины на карте меркаторской проекции

Рис. 4.1. Закон растяжения параллелей

В меркаторской проекции все меридианы и параллели прямые и взаимноперпендикулярные линии, а линейная величина каждого градуса широты постепенно увеличивается с возрастанием широты, соответственно растягиванию параллелей, которые все в этой проекции по длине равны экватору.

Принцип построения меркаторской проекции

Предложенная Меркатором проекция относится к разряду нормальных цилиндрических равноугольных проекций.

Карты, построенные в этой проекции, называются меркаторскими, а проекция - проекция Меркатора или меркаторская проекция.

Проекция Меркатора по характеру искажений относится к классу равноугольных.

Для получения морской навигационной карты в проекции Меркатора условный глобус помещают внутрь касательного цилиндра таким образом, чтобы их оси совпали.

Затем проецируют из центра глобуса меридианы на внутренние стенки цилиндра. При этом все меридианы изобразятся прямыми, параллельными между собой и перпендикулярными экватору линиями. Расстояния между ними равны расстояниям между теми же меридианами по экватору глобуса. Все параллели растянутся до величины экватора. При этом параллели, ближайшие к экватору, растянутся на меньшую величину и по мере удаления от экватора и приближения к полюсу величина их растяжения увеличивается.

Закон растяжения параллелей (рис. 4.1).


а)	б)	в)

R и r – радиус Земли и произвольной параллели (СС′).

φ – широта произвольной параллели (СС′).

Из прямоугольного треугольника ОС′К получим:

R = r · secφ

Обе части равенства умножим на 2π, получим:

2π · R = 2π · r · secφ

где	2π · R – длина экватора;
	2π · r – длина параллели в широте φ.

Следовательно, длина экватора равна длине соответствующей параллели, умноженной на секанс широты этой параллели. Все параллели, удлиняясь до длины экватора, растягиваются пропорционально secφ.

Разрезав цилиндр по одной из образующих, и развернув его на плоскость, получим сетку взаимно перпендикулярных меридианов и параллелей (рис. 4.1б).

Эта сетка не удовлетворяет требованию равноугольности, т.к. изменились расстояния между меридианами по параллели, ибо каждая параллель растянулась и стала равной длине экватора. В результате фигуры с поверхности Земли перенесутся на сетку в искаженном виде. Углы в природе не будут соответствовать углам на сетке.

Очевидно, для того, чтобы не было искажений, т.е. чтобы сохранить на карте подобие фигур, а следовательно, и равенство углов, необходимо все меридианы в каждой точке растянуть на столько, на сколько растянулись в данной точке параллели, т.е. пропорционально secφ. При этом эллипс на проекции вытянется в направлении малой полуоси и станет кругом, подобным острову круглой формы на поверхности Земли. Радиус круга станет равным большой полуоси эллипса, т.е. будет в secφ раз больше круга на поверхности Земли (рис. 4.1в).

Полученная таким образом картографическая сетка и проекция будут полностью удовлетворять требованиям, предъявленным к морским навигационным картам, т.е. проекцией Меркатора.

Из принципа построения меркаторской проекции видно, что все параллели картографической сетки вытягиваются пропорционально secφ и для сохранения равноугольности все меридианы этой сетки должны быть растянуты, в свою очередь, пропорционально растяжению параллелей, т.е. в secφ раз.

Чтобы построить картографическую сетку, удовлетворяющую требованию равноугольности, и учесть растяжение меридианов на величину secφ надо практически знать удаление по меридианам каждой параллели от экватора.

Удаление параллелей от экватора обычно выражается в экваториальных милях, так как экватор не испытывает растяжения и экваториальная миля → величина const.

Меридиональная часть (МЧ или D) → расстояние по меридиану от экватора до данной параллели, выраженное в экваториальных милях.

Если принимать Землю за шар, то МЧ вычисляется по формуле:

Для сфероида надо учесть сжатие Земли и формула для МЧ примет вид:

где	→ эксцентриситет эллипсоида вращения;
	а, в → большая и малая полуоси земного эллипсоида.

Вычисленные МЧ для эллипсоида даны в табл. 26 «МТ-75» (с. 280÷287) в экваториальных милях с точностью до 0,1 по аргументу φ с интервалом в 1′ или в табл. 2.28а «МТ-2000» (с. 314÷321).

Разность меридиональных частей (РМЧ) - расстояние по меридиану на проекции Меркатора между двумя параллелями, выраженное в экваториальных милях.

Меркаторская миля - РМЧ двух параллелей, отстоящих друг от друга на 1′.

Меркаторская миля является изображением на карте морской мили для данной широты (φ) и служит для измерения расстояний на карте.

Длина меркаторской мили изменяется с широтой (φ) пропорционально secφ несмотря на то, что величина морской мили остается во всех широтах постоянной.

Если в φ = 0° меркаторская миля изображается отрезком, равным экваториальной миле, то в φ = 60° она изобразится отрезком, равным 2-м экваториальным милям. То есть - измерять расстояния на карте в проекции Меркатора по вертикальной рамке в той же средней широте, где лежит измеряемый отрезок.

Единица карты - длина изображения одной экваториальной мили на меркаторской карте, выраженная в линейных мерах (длина изображения 1′ дуги параллели в проекции Меркатора).

Единица карты зависит от ее масштаба, который может быть отнесен к экватору или к любой выбранной параллели - главной параллели.

Построение меркаторской карты начинается с вычисления единицы карты. Если С_Э → главный масштаб по экватору, то единица карты (е) будет:

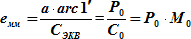
где	Р₀ – длина 1′ дуги главной параллели (φ₀) в мм, (для φ₀ = 60° → Р₀ = 0,502.168 (из табл. 6.3) · 1852.000 = 930.015)
	С₀ – знаменатель главного масштаба карты;
	М₀ = 1/С₀ – главный масштаб.

Таблица 4.2.- Длина минуты дуги меридиана и параллели (из табл. 2.29 «МТ-2000»)

φ°	Длина минуты меридиана (мили)	Длина минуты параллели (мили)	φ°	Длина минуты меридиана (мили)	Длина минуты параллели (мили)
0 2 4 6 8 10 12 14	0,995 107 0,995 119 0,995 155 0,995 216 0,995 300 0,995 408 0,995 539 0,995 692	1,001 812 1,001 206 0,999 388 0,996 361 0,992 127 0,986 692 0,980 062 0,972 244	46 48 50 52 54 56 58 60	1,000 299 1,000 650 1,000 999 1,001 343 1,001 682 1,002 013 1,002 335 1,002 647	0,697 125 0,671 586 0,645 221 0,618 063 0,590 145 0,561 499 0,532 162 0,502 168
16 18 20 22 24 26 28 30 32 34 36 38 40 42 44	0,995 866 0,996 062 0,996 277 0,996 510 0,996 762 0,997 030 0,997 313 0,997 610 0,997 919 0,998 239 0,998 568 0,998 906 0,999 249 0,999 597 0,999 947	0,963 487 0,953 085 0,941 764 0,929 301 0,915 708 0,901 003 0,885 201 0,868 322 0,850 385 0,831 410 0,811 422 0,790 442 0,768 496 0,745 610 0,721 810	62 64 66 68 70 72 74 76 78 80 82 84 86 88 90	1,002 947 1,003 232 1,003 503 1,003 758 1,003 994 1,004 213 1,004 410 1,004 588 1,004 743 1,004 876 1,004 985 1,005 071 1,005 132 1,005 170 1,005 182	0,471 554 0,440 358 0,408 617 0,376 370 0,343 657 0,310 518 0,276 995 0,243 128 0,208 959 0,174 530 0,139 885 0,105 066 0,070 117 0,035 080 0
	1,000 123	0,709 577

Таблица 4.2. позволяет рассчитать для проекции Меркатора единицу карты (е), модули параллелей (υ), частные масштабы (М) и линейный масштаб карты (μ).

Если при построении карты масштаб определяется тем условием, чтобы на карту поместился заданный район, то единица карты может быть рассчитана делением длины горизонтальной рамки карты (93 см или 68 см) на РД (Δλ) между крайними меридианами, выраженную в минутах.

Таким образом, сущность построения меркаторской карты состоит в том, что меридианы проводятся на расстояниях, пропорциональных РД (Δλ), с учетом масштаба, а параллели – на расстояниях, пропорциональных РМЧ, с учетом того же масштаба. Как РД, так и РМЧ выражены при этом в одних и тех же постоянных единицах – экваториальных милях.