Теорема Гаусса-Маркова

 

Согласно теореме Гаусса-Маркова, Метод наименьших квадратов, приведённый к линейному преобразованию матриц или к системе линейных уравнений, обеспечивает наилучшую несмещенную, эффективную и сходящуюся к пределу (“состоятельную”) оценку вектора параметров, т.е. наилучшее качество линейной модели, если соблюдаются условия (по [ 1 ]):

1. Линейная модель соответствует действительности.

2. Существует дисперсия регрессора.

3. Математическое ожидание возмущения равно нулю: E(u_i) = 0.

4. Возмущение имеет нормальное распределение.

5. Равенство ожидаемых значений дисперсий возмущений в разных диапазонах Х: E(u²) = Const. Это свойство называется гомоскедастичность, его несоблюдние – гетероскедастичность. Отклонение от гомоскедастичности проверяется по тесту Голдфелда-Квандта

GQ = Se₁²/Se₂² = ДИСП Ост1 / ДИСП Ост2

где ДИСП Ост1 и ДИСП Ост2– дисперсии остатков (отклонений) в первой и последней трети (или в половинах) диапазона Х; большая дисперсия делится на меньшую; GQ сравнивают с критерием Фишера для заданных уровня значимости и количества измерений; нормально GQ <4,35.

6. Отсутствие автокорреляции, т.е. взаимозависимости возмущений. Её оценивают, вычисляя статистикуДарбина-Уотсона остатков е:

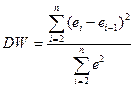
для которой вычислены критические значения при различных уровнях значимости и числе измерений. Приблизительно DW=0…1 означает положительную автокорреляцию, 3…4 отрицательную автокорреляцию, DW=1,5…2,5 позволяет принять гипотезу об отсутствии автокорреляции, DW=1…1,5 и DW=2,5…3 не позволяют принять гипотезу о наличии или отсутствии автокорреляции. Наличие автокорреляции означает, что аппроксимирующая функция подобрана неверно, или же требуется применение других методов и моделей. Автокорреляция разобрана в разделе …

Статистику Дарбина-Уотсона можно вычислить по формуле

DW = 2(1-Rавт),

где Rавт - коффициент автокорреляции, вычисляемый с помощью функции КОРРЕЛ: задать в окне Массив1 диапазон остатков с номерами 1 : n-1, а в окне Массив2 диапазон 2 : n.

Понятия “гетероскедастичность” и “автокорреляция” актуальны, если массивы данных упорядочены, что имеет место для временных рядов. “Пространственные” данные можно искусственно упорядочить, например, отсортировав их по возрастанию какой-либо переменной; при этом можно выявить кластеры с аномальной дисперсией остатков, что может означать неоднородность выборки или неадекватность модели.

Контрольные вопросы.

1. Общий вид уравнений парной и множественной регрессии.

2. Нелинейные уравнения регрессии.

3. Формулы для вычисления коэффициентов парной линейной регрессии и их погрешностей.

4. Метод наименьших квадратов (МНК) и система нормальных уравнений парной линейной регрессии.

5. Матричный метод МНК

6. Теорема Гаусса-Маркова: формулировка и условия.

7. Показатели качества эконометрической модели: коэффициент детерминации R², статистика Фишера F, t-статистики Стьюдента для коэффициентов уравнений.

8. Показатели качества эконометрической модели: тест Дарбина-Уотсона на автокорреляцию DW, тест Голдфелда-Квандта на гетероскедастичность GQ.

9. Гетероскедастичность случайного возмущения. Причины, последствия.

10. Что такое ВМНК и ОМНК и когда они применяются.