Случайные погрешности
Случайная погрешность 
измерений определяется как разность между измеренным результатом 
измерения и истинным значением Х измеряемой величины
. (3.12)
Для каждого 
-ого измерения 
случайная погрешность вычисляется по формуле
. (3.12*)
Поскольку истинное значение измеряемой величины определить невозможно в процессе выполнения измерений на практике необходимо дать оценкупогрешности результатов измерений и установить границы измеряемой величины.
Для оценки результатов измерений, содержащих случайные погрешности, пользуются понятиями и методами теории вероятностей и математической статистики, поскольку закономерности в появлении этих значений нет
Результат отдельного наблюдения при многократном прямом измерении какой-либо физической величины из-за наличия случайных погрешностей представляет собой случайную величину.
Случайнойв математике называют такую величину, которая в зависимости от случая принимает то или иное численное значение. Для характеристики случайной величины необходимо знать совокупность возможных значений этой величины, а также вероятности, с которыми эти значения могут появляться.
Вероятность события является количественной оценкой объективной возможности его появления. Вероятность достоверного события равна единице, а вероятность невозможного события – нулю. События, вероятности появления которых больше нуля и меньше единицы, являются событиями случайными.
Применительно к области измерений можно считать, что при проведении равноточных наблюдений каждая из множества возможных незначительных причин случайных изменений результатов может появиться или не появиться. В итоге случайные измерения появляющиеся при каждом измерении, могут быть любыми как по размеру, так и по знаку.
Для дискретной случайной величины наиболее полной статистической характеристикой является ее распределение вероятностей: указываются возможные значения этой величины xi и соответствующие им вероятности Рi. Расположив значения хi, …, xn в порядке возрастания и обозначив вероятности P1, …,Рn , получим график распределения вероятностей этой дискретной величины (рисунок 3.7). Сумма всех вероятностей равна единице. Наиболее вероятное значение дискретной случайной величины называется модой (величина х6 на рисунке 3.7).
Рисунок 3.7 - Распределение вероятностей дискретной случайной величины
Значения непрерывной случайной величины могут отличаться друг от друга сколь угодно мало, поэтому вероятность каждого из этих значений также бесконечно мала, и построить кривую распределения вероятностей невозможно. Чтобы выявить распределение вероятностей в этом случае, рассматривают некоторое множество интервалов в диапазоне возможных значений хi случайной величины и подсчитывают частоты mi попадания значений хi в каждый из этих интервалов, получая таким образом статистический ряд.. Расположив, значения хi в порядке возрастания (таблица 3.1) и обозначив соответствующие им вероятности Р, получим ступенчатую кривую — гистограмму (рисунок. 3.8,а).
Таблица 3.1 - Построение статистического ряда случайной величины
| Интервал хi | 
| 
| … | 
|
Частота 
| 
| 
| … | 
|
Если взять бесконечно малые интервалы (т.е. произвести интегрирование), график потеряет ступенчатый характер и преобразуется в плавную кривую, называемую кривой распределения плотности вероятности Pk для данной непрерывной случайной величины - (штриховая линия на рисунке 3.8,а). Уравнение, описывающее эту плавную кривую, называется законом распределения данной непрерывной случайной величины.
Рисунок 3.8 - Построение гистограммы распределения случайной величины
Ордината кривой (например 
в точке 
на рисунке 3.8,б) называется плотностью вероятности в данной точке. Площадь же под всей кривой равна вероятности появления любого из возможных значений , т.е. единице.
Модой для непрерывной случайной величины называется максимальное значение распределения.
Большинство случайных величин распределяются по нормальному закону распределения (рисунок 3.9). Согласно этому закону плотность распределения вероятностей для любой случайной величины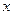 
описывается уравнением
, (3.13)
где 
- среднее квадратическое отклонение случайной величины (результата отдельного измерения) от её математического ожидания 
.
Это выражение применимо и к распределению случайных погрешностей
, (3.14)
где 
- среднее квадратическое отклонение погрешности от её математического ожидания 
.
Случайные погрешности многократных измерений обычно распределены по нормальному закону даже если законы распределения вероятностей составляющих отличаются от нормального.
На рисунке видно, что кривые нормального распределения симметричны относительно opдинаты, проходящей через точку, соответствующую моде и имеют в этой точке единственный максимум, равный 1/(
) (мода для нормального закона распределения). При = 0 кривая симметрична относительно оси ординат. Абсциссам - 
и + соответствуют точки перегибов кривой, с уменьшением максимум кривой возрастает и она становится более островершинной.
1 – для s1; 2 – для s2; 3 – для s3
Рисунок 3.9 – Нормальное распределение плотности вероятности
случайной величины: s1>s2>s3
Нормальное распределение бесконечно большой совокупности непрерывных случайных величин было исследовано К.Ф.Гауссом (поэтому нормальное распределение называют еще гауссовым). Использование распределения Гаусса для обработки конечных совокупностей случайных величин также возможно, если число их n достаточно велико (n > 30). В этом случае условно считают, что наблюдаемые n значений величины x, т.е. x1, х2, …, хn представляют собой случайную выборку из воображаемой бесконечной генеральной совокупности. Понятие бесконечной генеральной совокупности есть математическая абстракция: генеральной называют совокупность всех мыслимых наблюдений, которые могли бы быть сделаны при данном комплексе условий. Сущность методов математической статистики состоит в том, чтобы по некоторой части генеральной совокупности (по выборке объема n) вынести суждение о свойствах всей совокупности в целом. При большом числе наблюдений, каждое из которых даёт случайный результат, взаимно уравновешиваются влияния случайных факторов и проявляются общие закономерности, которые позволяют описать данную генеральную совокупность в виде некоторых усредненных величин.
В статистике малых выборок (в микростагистике) большую роль играет другое распределение непрерывных случайных величин - распределение Стьюдента. График распределения Стьюдента напоминает по форме нормальное распределение и с увеличением n приближается к нему все больше (можно считать, что при n > 30 оба графика практически совпадают).
Для практических целей вместо полного статистического описания свойств генеральной совокупности случайных величин х с помощью закона их распределения P(x) часто ограничиваются только указанием некоторых частных характеристик совокупности - моментов распределения (начальных и центральных).
Начальным моментом к-того порядка случайной величины х называют математическое ожидание (теоретическое среднее значение) к - той степени ее:
. (3.15)
Среди начальных моментов наиболее важным является первый:
. (3.16)
Первый начальный момент характеризует положение центра распределения — точки, к которой тяготеет совокупность значений случайной величины х (значение х-координаты центра тяжести фигуры, образованной осью абсцисс и кривой распределения этой случайной величины).
Центральным моментом k-го порядка (k-тым центральным моментом) случайной величины х называют математическое ожидание степени ее отклонения от среднего значения:
(3.17)
Первый центральный момент всегда равен нулю, так как
.
Второй центральный момент m2(х), характеризующий рассеивание случайной величины х, разброс ее значений относительно центра группирования называется дисперсией D (х).
Для непрерывной случайной величины дисперсия
. (3.18)
Размерность дисперсии отлична от размерности исследуемой случайной величины х, поэтому вместо нее часто применяют положительный корень из дисперсии, который называют стандартным отклонением, стандартом или средним квадратичным отклонением (СКО):
. (3.19)
Для случайной величины, распределенной по нормальному закону, математическое ожидание М(х) и среднее квадратическое отклонение 
совпадают соответственно с параметрами M(x) и s(х) из формулы (3.13). Поэтому принято среднее квадратическое отклонение обозначать символом s(х), причем и саму дисперсию D(x) нередко обозначают как s2(х).
Для описания распределений иногда используют третий и четвертый центральные моменты.
Третий центральный момент m3(x) характеризует отклонение кривой распределения от симметричной. Асимметрией называют величину
. (3.20)
Для симметричного распределения А(x)=0. При А(х)>0 асимметрия правосторонняя (правая ветвь более вытянута, спуcкается от вершины менее круто, чем левая), при А(х)<0 левосторонняя (правая ветвь более крутая, а левая - пологая, удлиненная).
Четвертый центральный момент m4(x)характеризует островершинность кривой распределения. Эксцессом называется величина
(3.21)
Поскольку для нормального распределения 
, то эксцесс отображает островершинность по сравнению с кривой нормального распределения: при Е(х)>0 данная кривая более островершинна, а при Е(х)<0 - менее островершинна, чем нормальная.
Вычисления mk производятся по формулам (3.22 – 3.24). Значения mk находят по формулам
; (3.22)
; (3.23)
. (3.24)
Способы статистического описания свойств случайных величин относятся к их генеральной, бесконечной совокупности. Поскольку на практике число n наблюдаемых значений величины x ограничено, по данным такой случайной выборки x1, х2, …, хn определить истинные значения неизвестных параметров распределения М(х) и 
невозможно. Вместо них определяются только их статистические оценки 
и 
, которые, являясь функциями членов выборки, отклоняются от истинных значений соответствующих параметров. Статистическая оценка называется точечной, если ее значение можно представить геометрически в виде точки на координатной оси, по которой откладываются значения однородной случайной величины.
По степени совершенства статистические оценки характеризуются состоятельностью, несмещенностью и эффективностью.
Состоятельная оценка при увеличении объема выборки приближается к истинному значению величины.
Несмещеннойназывают оценку, математическое ожидание которой равно истинному значению величины. Несмещенную состоятельную оценку часто удается получить из смещенной состоятельной оценки, умножая последнюю на некоторую функцию от n.
Эффективная оценка обладает минимальной дисперсией по сравнению с другими оценками.
Математическое ожидание случайной величины (погрешности)– это такое её значение, вокруг которого группируются результаты отдельных измерений (погрешностей).
Статистической оценкой истинного значения математического ожидания случайной величины является среднее арифметическое выборки
. (3.25)
Эта оценка является состоятельной и несмещенной для любого закона распределения случайных величин; при нормальном законе распределения она и эффективна.
Рассеяние результатов в ряду измерений- несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.
Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей и определения 
по формуле (3.25).
Оценками рассеяния результатов в ряду измерений могут быть:
- размах,
- средняя арифметическая погрешность (по модулю),
- средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение),
- доверительные границы погрешности (доверительнаяграница или доверительная погрешность).
Размах результатов измерений- оценка рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из п измерений), вычисляемая по формуле
= xmax - xmin, (3.26)
где доверительный интервал с границами 
и
,хmax и xmin - наибольшее и наименьшее значения физической величины в данном ряду измерений.
Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер.
При большом числе n значений случайной величины х в выборке оценку их СКО можно вычислить по формуле (для любого закона распределения, а не только для нормального)
. (3.27)
Эта оценка характеризует сходимость результатов – степень их концентрации относительно центра распределения погрешностей. Величина 
- оценка состоятельная, но при малых объемах выборки – смещенная.
Средняя квадратическая погрешностьрезультатов единичных измерений в ряду измерений - оценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, вычисляемая по формуле Бесселя
, (3.28)
где хi - результат i-го единичного измерения, 
- среднее арифметическое значение измеряемой величины из п единичных результатов.
Как видим, формула (3.28) получена путем умножения подкоренного выражения в формуле (3.27) на поправочный множитель n/(n –1), что дает уменьшение смещенности. Данная оценка является состоятельной, но не эффективной. Она лишь асимптотически эффективна, т.е. её собственное рассеяние относительно стремится к минимальному при неограниченном увеличении числа n значений х в выборке, но все же составляет несколько процентов при очень больших n. Поэтомузначения 
больше чем с двумя значащими цифрами не записывают.
Важно. На практике широко распространен термин среднее квадратическое отклонение - (СКО). Под отклонением в соответствии с формулой (3.28) понимают отклонение единичных результатов в ряду измерений от их среднего арифметического значения. В метрологии это отклонение называется погрешностью измерений. Если в результаты измерений введены поправки на действие систематических погрешностей, то отклонения представляют собой случайные погрешности. Поэтому с точки зрения упорядочения совокупности терминов, родовым среди которых является термин «погрешность измерения», целесообразно применять термин «средняя квадратическая погрешность» (СКП). При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов единичных измерений.
Средняя квадратическая погрешность результата измерений среднего арифметического– оценка случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений, вычисляемая по формуле
.(3.29)
Из этой формулы видно, что точность 
как оценки математического ожидания случайной величины возрастает с увеличением объема выборки n асимптотически, поэтому на практике число наблюдений при одном значении измеряемой величины не превышает 10.
Доверительные границы погрешности результата измерений и- наибольшее и наименьшее значения погрешности измерений, ограничивающие доверительный интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений. При симметричных границах термин может применяться в единственном числе - доверительная граница.
Иногда вместо термина доверительная граница применяют термин доверительная погрешность или погрешность при данной доверительной вероятности.
Доверительный интервал включает истинное значение 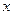измеряемой величины с доверительной вероятностью
, (3.30)
где 
- функция Лапласа (интеграл вероятности), значения которой табулированы,
. (3.31)
Вероятность того, что случайная погрешность окажется за границами интервала , равна
(3.32)
и называется уровнем значимости.
На практике довольно часто ограничиваются доверительным интервалом от 
до 
, для которого доверительная вероятность составляет 0,9973 или 99,73%.
Пример -При измерении силы тока среднее квадратическое отклонение составило 0,2 % (
). Определить вероятность того, что случайная погрешность измерения будет лежать в пределах доверительного интервала ±0,5%.
Решение:
1) Границы интервала 
.
2) По формуле (3.31) имеем 
.
3) Для 
.
4) Уровень значимости 
.
Пример - Определить границы доверительного интервала при измерении силы тока для 
, если доверительная вероятность равна 0,995.
Решение:
1) Для 
.
2) Доверительный интервал 
.
3) Случайная погрешность может достигнуть значений 
.
Доверительный интервал для случайной погрешности среднего значения 
, соответствующий выбранной доверительной вероятности 
, определяют по формуле
, (3.33)
где
. (3.34)
Пример - Определить доверительный интервал для среднего значения сопротивления нагрузки по результатам 64 наблюдений при 
и доверительной вероятности Р=0,9 (90 %).
Решение:
1) Среднее квадратическое отклонение 
.
2) Для 
.
3) Границы доверительного интервала 
.
4) Погрешность измерений с вероятностью 90 % не будет превышать 
.
При малом числе наблюдений, когда неизвестно , доверительную вероятность и доверительный интервал определяют, пользуясь законом распределения Стьюдента, которое характеризуется коэффициентом t и находится по специальным таблицам.
Зная число наблюдений n и задавшись доверительной вероятностью, находят значение коэффициента Стьюдента ts по соответствующим справочным таблицам, выдержка из которых приведена в таблице 3.2.
Если значения случайной величины х подчиняются нормальному распределению, доверительный интервал симметричен относительно точечной оценки , и тогда можно записать
. (3.35)
Таблица 3.2 – Значение коэффициента tS для случайной величины X, имеющей распределение Стьюдента с n-1 степенями свободы
| n-1 | Р=0,95 | Р=0,99 | n-1 | Р=0,95 | Р=0,99 |
| 3,182 | 5,841 | 2,120 | 2,921 | ||
| 2,776 | 4,604 | 2,101 | 2,878 | ||
| 2,571 | 4,032 | 2,086 | 2,845 | ||
| 2,447 | 3,707 | 2,074 | 2,819 | ||
| 2,365 | 3,499 | 2,064 | 2,797 | ||
| 2,306 | 3,355 | 2,056 | 2,779 | ||
| 2,262 | 3,250 | 2,048 | 2,763 | ||
| 2,228 | 3,169 | 2,043 | 2,750 | ||
| 2,179 | 3,055 | ∞ | 1,960 | 2,576 | |
| 2,145 | 2,977 |
Пример - Шестикратное измерение сопротивления резистора дало следующие результаты: 72,361; 72,357; 72,352; 72,346; 72,344; 72,340 Ом. Определить доверительный интервал при Р=0,99.
Решение:
1) Среднее арифметическое 
.
2) Сумма отклонений от среднего равна 
.
3) 
,
.
4) Для 
и 
из таблицы 3.2 коэффициент Стъюдента t =4,03.
5) Доверительный интервал для среднего
.
6) Результат измерения следует представить в виде
.
Статистический критерий обнаружения грубых погрешностей имеет вид
, (3.36)
при выполнении которого результат отбрасывается как анормальный. Значения коэффициента 
при некоторых значениях n приведены в таблице 3.3.
Таблица 3.3 - Значения коэффициента
|
| |||
| 0,100 | 0,075 | 0,050 | 0,025 | |
| 1,15 | 1,15 | 1,15 | 1,15 | |
| 1,7 | 1,79 | 1,85 | 1,93 | |
| 2,03 | 2,10 | 2,18 | 2,29 | |
| 2,36 | 2,46 | 2,56 | 2,71 |
Пример - Имеется 10 значений, составляющих статистический ряд наблюдений при измерении сопротивлений R: 9,992; 9,995; 9,997; 9,9999; 10,000; 10,001; 10,003; 10,005; 10,007; 10,121. Подозрительным является результат 
. Его и надо проверить по критерию (3.36).
Решение:
1) Среднее значение 
.
2) Среднее квадратическое отклонение
.
3) Значение критерия равно
.
4) При 
и всех значениях уровня значимости (см. таблицу 3.4) 
, поэтому 
отбрасываем как грубую погрешность. Дальнейший расчет ведем по алгоритму предыдущего примера при n=9.
Суммарная средняя квадратическая погрешность результата измерений(суммарная погрешность) - погрешность результата измерений (состоящая из суммы случайных и неисключенных систематических погрешностей, принимаемых за случайные), вычисляемая по формуле
, (3.37)
где
- средняя квадратическая погрешность суммы неисключенных систематических погрешностей рассчитанных по (3.10 или 3.11) при равномерном распределении (принимаемых за случайные).
Доверительные границы суммарной погрешности могут быть вычислены по формуле
, (3.38)
где
, (3.39)
где 
- граница суммы неисключенных систематических погрешностей результата измерений, вычисляемая по формулам (3.10) или (3.11); 
- доверительная граница погрешности результата измерений по (3.35).