Коэффициент детерминации

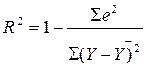( 3.1 )

Для линейной модели он совпадает с квадратом коэффициента корреляции, но пригоден и для нелинейных моделей. На Рисунке 3.2. показана аппроксимация параболой. Коэффициент корреляции близок к нулю, а коэффициент детерминации – к единице, так как дисперсия Рис.3.2.

остатков существенно меньше дисперсии Y. Это говорит о высоком качестве модели.

Формула ( 3.1 ) легко преобразуется

(3.2)

 

где ДИСП – функция Excel Дисперсия. Вообще говоря, несмещённой оценкой дисперсии остатков парной регрессии является

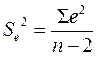
но функция ДИСП.В делит на (n-1), и в данном случае всё получается правильно. В данном случае r² = 0,854, что соответствует коэффициенту корреляции 0,924, то есть имеет место сильное влияние переменной X на Y.

Дисперсия суммы двух независимых переменных равна сумме их дисперсий. В Таблице вы видите, что ДИСП(Y)=ДИСП(Y^) + ДИСП(е).

Надо сказать, что S(Y – Ycp)² обозначают TSS (Total Squared Sum); в российских учебниках S(Y^ – Y^cp)² обозначают RSS, а Sе² ESS (Error Squared Sum; в английских учебниках S(Y^ – Y^cp)² обозначают ESS (Explained Squared Sum) а Sе² RSS (Residual Squared Sum). Поэтому мы не будем пользоваться этими обозначениями.

Оценка значимости уравнения регрессии в целом даётся с помощью F-критерия Фишера. При этом проверяется нулевая гипотеза, что коэффициент регрессии b равен нулю и, следовательно, фактор X не оказывает влияния на результат Y. Давно составлены таблицы критических значений F-статистики в зависимости от числа измерений n, числа степеней свободы, или количества независимых переменных m и уровня значимости a.

Статистика Фишера равна частному от деления дисперсии Y^, или факторной дисперсии, и дисперсии остатков, вычисленных с учётом числа степеней свободы: 1 для Y^ и n-2 для остатков.

Для множественной регрессии и полиномиальной, которую можно преобразовать в множественную, число степеней свободы Y^ равно числу независимых переменных m, а число степеней свободы остатков равно n-m-1. Статистику Фишера удобно вычислять через коэффициент детерминации:

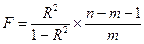( 3.3 )

Чем больше статистика Фишера, тем лучше прогнозы, сделанные с использованием модели. Из формулы (3.3) следует, что F возрастает с ростом r² и числа измерений, но уменьшается при увеличении числа влияющих переменных, то есть надо аккуратно подходить к включению в модель новых влияющих переменных, а также не использовать для аппроксимации полиномы высоких степеней. Полезно помнить, что при уровне значимости a=0,05, то есть при доверительной вероятности 95% и количестве замеров более 15 критическое значение F для парной регрессии около 4,5 , а при m=4 около 3. Начиная с этих значений F можно говорить о существовании влияния регрессоров на эндогенную переменную.

Коэффициенты линейного уравнения регрессии b_i имеют экономический смысл: это предельные функции, или производные эндогенной переменной по влияющим:

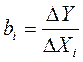
В случае парной регрессии это однозначно, в множественной регрессии всё сложнее из-за взаимного влияния регрессоров. Для оценки погрешностей коэффициентов уравнения парной линейной регрессии Y^= a + bx используются выражения

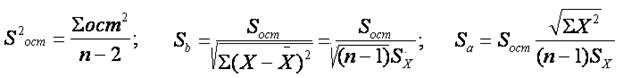где S – выборочные оценки стандартных отклонений s. Для принятия гипотезы о влиянии регрессора на эндогенную переменную используются таблицы критических значений t-статистики Стьюдента. Для bt=b/S_b. Предполагается, что при числе измерений больше 20 истинные значения коэффициентов уравнения регрессии aи b лежат в интервалах {a-2S_a , b+2 S_b } и {b-2S_b , b+2 S_a } с доверительной вероятностью 95%.