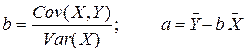Множественная регрессия представляет собой модель, где ожидаемое значение зависимой переменной y рассматривается как функция многих объясняющих переменных, то есть модель вида
Е(y) =f(x1, х2, …, xn)
Случайную переменную у формируют функция f(x) и случайная величина u (uncertainty, disturbance term, возмущение) с ожидаемым значением, равным нулю:
у = f(x)+и
Такое разложение случайной переменной уименуется регрессионным анализом переменной у.
Предполагается, что f(x) отражает идеальную закономерность, на которую накладываются неучтённые факторы или ошибки измерения. В физике это так, а в экономике – нет. В физике параметрами функции f(x) являются константы, которые надо оценить по результатам измерений (скорость света, масса протона, период полураспада радиоактивного изотопа). В экономике измеряемые величины (ВВП, количество населения) и их взаимосвязи постоянно меняются, поэтому нет фундаментальных констант. Тем не менее, эконометрика переняла математический аппарат, разработанный для физики, и мы его будем использовать.
Регрессионные модели, которые наиболее часто используются в эконометрике:
1) Линейная y = a + bx+u; употребляется наиболее часто, остальные функции стараются преобразовать к линейному виду, линеаризовать.
Регрессии, нелинейные относительно включённых в анализ объясняющих переменных:
2) Полином второй, редко третьей степени y = a + bx+сх2+u.
3) Равносторонняя гипербола y = a +b/x +u.
Эти модели сводятся к линейным заменой переменных: z = х2 для полинома и z=1/x для гиперболы.
К нелинейным регрессиям по оцениваемым параметрам относятся:
4) Степенная y = axbe;
5) Показательная y = abxe;
6) Экспоненциальная y = ea+bxe.
Здесь e =1+ u. Эти модели могут быть линеаризованы логарифмированием.
Следует отметить разницу между идеальной закономерностью, которую для линейной модели обычно записывают
y = a + bx+u
и оценённой регрессионной моделью
y = a +bx + e,
а также возмущением u и отклонением, или ошибкой е. Предполагается, что a и b являются реальными константами, а a и bслужат их оценками. В экономике констант нет, но математический аппарат сохраняется. Возмущение u – это отклонение реального замера от идеальной закономерности a+bх, которую мы не знаем. Значит, u мы тоже не знаем, но можем делать предположение о его свойствах. Ошибка е – это разность между реальным у и его значением, оценённым по формуле a + bx; она служит оценкой u.
Коэффициенты b и a можно вычислить по формулам