Ее дисперсия и среднее квадратическое отклонение

 

Важную роль играют две количественные харак­теристики случайной переменной х: математическое ожидание (ожидаемое значение) и дисперсия. Ожидаемое зна­чение, которое обычно обозначают m, m или Е(х) находится по формуле

( 2.1 )

Подчеркнем, что m– это константа, вокруг которой рассеяны возможные значения q случайной переменной х.

Дисперсия s², Var(x) – это математическое ожидание квадрата отклонения случайной переменной х от её ожидаемого значения:

 

( 2.2 )

 

 

Положительный квадратный корень из дисперсии 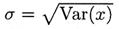именуется средним квадратическим отклонением (СКО), или стандартным отклонением. Размерно­сти s и х совпадают. Величина s (как и s²) служит характеристикой неопределенности (изменчивости) х. Формула ( 6.26) может быть преобразована к виду

s² = Е(х²) - m² ( 2.3 )

Из формул (6.25)-(6.27) видно, что для отыскания величин m, s нужно знать закон распределения P_x(q) случайной пере­менной х. Часто это закон неизвестен, и тогда можно оценить (приближенно определить) характеристики m, s² по результатам n независимых наблюдений (опытов)

{ х₁, х₂, …, х_n}. В этом наборе каждая компонента х_i – это случайная пере­менная с одним и тем же законом распределения P_x(q), при этом величины х_i являются независимыми.

Можно выделить три уровня параметров случайной величины:

1. Результаты замеров реально существующей константы. Примеры: масса протона, период полураспада (или вероятность распада) радиоактивного изотопа, вероятность падения монеты орлом кверху. Эти константы объективно существуют, и, проводя эксперименты, мы можем приближаться к ним, достигая заданной точности. Увеличивая число бросков монеты, мы можем сделать оценку вероятности выпадения орла сколь угодно близкой к 1/2. В экономике и социологии абсолютных констант не существует, нет абсолютно точных взаимозависимостей величин, как в физике. Существуют константы, устанавливаемые правительством, например, ставка налога, но они не являются фундаментальными, могут меняться, и их не оценивают с использованием статистики и эконометрики.

2. Роль абсолютных констант, характеризующих экономику и социальную сферу страны и региона играют параметры генеральных совокупностей – всех доступных значений по стране или региону. Примеры: средний доход домохозяйств, процент заболевших гриппом. В принципе, эти параметры можно измерить во время переписей населения или тотальных проверок (при условии достоверной информации), но такие технологии дороги, а исследуемые параметры непрерывно меняются. Поэтому для оценки параметров природных и социально-экономических объектов служат случайные выборки.

3. Случайные выборки. Было доказано, что если замеры х независимы, то наилучшая оценка математического ожидания Е(х) – среднее значение по выборке

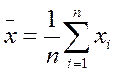
( 2.4 )

 

а наилучшая оценка дисперсии s²

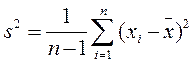
( 2.5 )

 

Почему n-1, а не n? Дело в том, что в формуле ( ), используется не математическое ожидание Е(х), которое мы не знаем, а его оценка – среднее значение 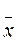, вычисляемое по выборке Х{ х₁, х₂, …, х_n}, поэтому смещённое относительно Е(х) и расположенное ближе к центру значений множества { х₁, х₂, …, х_n}. Если делить на n, получим заниженную оценку дисперсии. n в формуле ( ) и n-1 в формуле ( ) – это число степеней свободы, независимых суммируемых переменных. Поскольку 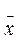вычислено по { х₁, х₂, …, х_n}, одно из выражений в скобках в формуле ( 2 ) мы можем вычислить, зная n-1 значений х.

Что такое наилучшая оценка, или наилучшая технология оценки (estimator) математического ожидания? Каковы её критерии?

1. Несмещенность. Применяя правильную технологию расчёта, мы не получим в результате обработки серии замеров статистически значимого отклонения от реального значения оцениваемого параметра.

2. Эффективность. Если в формуле (…) мы используем вместо 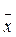другую величину, полученную по другой формуле, то дисперсия (…) будет больше. Значит, среднее значение обеспечивает наиболее эффективную оценку математического ожидания Е(х). Эффективность может вступить в противоречие с несмещённостью. Например, исключение переменных из эконометрических моделей может привести к уменьшению дисперсий оцениваемых параметров и к их смещению относительно истинных значений.

3. Consistency. В российских учебниках это слово переводят как “состоятельность”, но правильнее говорить о сходимости. Это значит, что увеличивая количество замеров в серии n, мы можем получить разность оценок исследуемого параметра меньше любого e (вспомнили матанализ?), то есть наши оценки сходятся к какому-то пределу.

В технических вузах проводят лабораторную работу: дают студентам одинаковые детали и микрометр. Студенты измеряют размеры деталей и строят гистограммы частотных распределений, то есть считают количество деталей в каждом интервале размеров.

 

 

Рис.1. Гистограмма частотного распределения и кривая Гаусса с параметрами Е(х) = 0 и s = 1.

 

 

Инженеры считают, что размеры деталей подчиняются закону нормального распределения (ЗНР), выведенного К.Гауссом

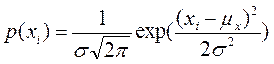
Как видите, в функции Гаусса всего два параметра: математическое ожидание Е(х) и стандартное отклонение s, которые сравнительно легко оценить по выборке, используя формулы (.. ) и ( ). Эти формулы реализованы в Excel в функциях соответственно СРЗНАЧ, ДИСП и СТАНДОТКЛОН, категория «Статисти­ческие». Зная параметры гауссианы, можно вычислить процент деталей в различных диапазонах х (квантили), используя таблицы или функцию НОРМРАСПР Excel. Поэтому закон нормального распределения широко применяется при проектировании машин и механизмов. Например, можно вычислить количество событий (деталей) в диапазоне {Е(х) -2s, Е(х) +2s}. Это примерно 95%, то есть в “хвостах” останется по 2,5%. В данном случае р = 0,95 – доверительная вероятность, а {Е(х) -2s, Е(х) +2s} - соответствующий доверительный интервал. В общем виде это утверждение выглядит следующим образом: для уровня значимости a = 1– р доверительный интервал равен {Е(х) – t_критs, Е(х) + t_критs}, где t_крит – критические значения статистики Стьюдента t = Е(х)/s. В нашем примере a – доля деталей в “хвостах”. При уменьшении числа замеров надёжность оценки Е(х) и дисперсии падают, и доверительный интервал надо расширять. Поэтому критические значения статистики Стьюдента зависят от уровня значимости (доверительной вероятности) и количества замеров (степеней свободы). Распределение Стьюдента t_крит(a, n) приведено во всех учебниках и практикумах по математической статистике и эконометрике. В Excel имеется функция СТЬЮДРАСП(t_крит, n, число хвостов (1 или 2)), которая возвращает долю событий в “хвостах”. Для практических целей достаточно запомнить, что при числе замеров больше 20 и р=95% t_крит примерно равно 2. Инженеры используют правило, опирающееся на распределение Гаусса: “за тремя сигмами ничего нет”, то есть количество деталей с размерами, отклоняющимися от среднего более чем на 3s, ничтожно мало, меньше 0,15% в каждом “хвосте” (сейчас переходят на шестисигмовый уровень надёжности). Разница экономики и техники состоит в том, что 5% невыгодных сделок – не страшно, а 5% или 2,5% (один хвост) заклиненных деталей – это много.

return false">ссылка скрыта

В метеорологии, геохимии, биологии и экономике закон нормального распределения не работает, что связано с когерентностью, то есть взаимной зависимостью событий. Например, изъятие вкладов из банка может многократно превысить средний уровень из-за негативных публикаций или слухов. Для природы и экономики характерны распределения “с толстыми хвостами”, то есть количество аномальных замеров достаточно велико. Известно, что количество природных катастроф в зависимости от количества жертв подчиняется экспоненциальному закону. Успешно используется логнормальное распределение, сводимое к нормальному заменой x_i на log(x_i). Логнормальному распределению подчиняются, по данным автора, микроэлементы и чернобыльские радионуклиды в пробах, количество покупок в магазине в зависимости от их стоимости.

Автор не располагает данными о количестве льготников – пассажиров на городском и пригородном транспорте, но предполагает, что именно незнание законов частотных распределений в социальной сфере привело к бунтам и блокированию трасс при монетизации льгот. Предположим, что количество льготников N в зависимости от стоимости проезда распределено по логнормальному закону (Рис.8). По оси абсцисс указано количество поездок на городском транспорте в день.

Рис.8. Количество льготников N в зависимости от стоимости проезда.

 

Видимо, при расчетах компенсаций был использован закон нормального распределения (плавная кривая), компенсировали средние затраты, но больше половины льготников были недовольны. Даже когда добавили σ, потом 2σ, может быть 3σ, то осталось много недовольных: бывшие военные, полярники, милиционеры, которые ездят из пригородов в Москву на заработки. В результате – огромные траты из казны, а льготный проезд из пригородов пришлось оставить.

В математической статистике используются также распределения Пирсона (хи-квадрат), Фишера, Стьюдента.

Одна из основных задач эконометрики – выявление взаимосвязи переменных. Количественными оценками взаимосвязи служат ковариация и коэффициент корреляции. Ковариация переменных x и y – это ожидаемое значение произведения их отклонений от ожидаемых значений:

сov(x,y) = E((х-E(х))(y-E(y)))

 

Для оценки ковариации по выборке используется формула, аналогичная формуле дисперсии

 

Cov(x,x) – это дисперсия x. Коэффициент корреляции – это ковариация, нормированная на стандартные отклонения x и y:

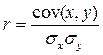
Коэффициент корреляции – безразмерная величина, изменяется от –1 до +1; близость к нулю означает отсутствие связи переменных.

Проведите обработку простого массива данных X и Y. Вычислите количество данных, используя функцию Excel СЧЁТ(). До 11 мы считать умеем, но реальные таблицы экономических данных могут быть огромными. Вычислите суммы X и Y, используя функцию S, и их средние значения, используя формулу и функцию СРЗНАЧ(). Вычислите квадраты отклонений X и Y от их средних значений, просуммируйте. Обратите внимание на фиксацию адресов Xcp и Ycp знаком $. Вычислите дисперсии и среднеквадратические отклонения (СКО) по формулам и через функции ДИСП и СТАНДОТКЛОН. Сравните результаты. Вычислите ковариацию и корреляцию по формулам и через функции КОВАР и КОРРЕЛ.

	X	Y	(X-$Xcp)^2	(Y-$Ycp)^2	(X-$Xcp)* (Y-$Ycp)
				109,2	52,2
				55,5	29,8
				19,8	13,3
				41,6	12,9
				2,38	-1,54
				0,20
				20,6	4,54
				30,7	11,0
				6,47	7,63
				91,1	38,1
				30,7	27,7
N СЧЁТ()
Sum				408,7
Среднее Sum/N		22,45
Среднее СРЗНАЧ		22,45			Ковариация
Дисперсия		Sum(X-$Xcp)^2 /(N-1)		40,8	19,6
СКО(Sx,Sy)		КОРЕНЬ	3,31	6,39
СКО		СТАНДОТКЛОН	3,31	6,39	Корреляция
				Cov/Sx/Sy	0,924
				КОРРЕЛ()	0,924

 

Контрольные вопросы

1. Дифференциальный и интегральный закон распределения случайной величины, виды функций распределения. Что такое “толстые хвосты”?

2. Параметры случайной величины: ожидаемое значение, дисперсия и среднее квадратическое отклонение, коэффициенты ковариации и корреляции.

3. Проверка статистических гипотез, t-статистика Стьюдента, доверительная вероятность и доверительный интервал, критические значения статистики Стьюдента.