Преобразование Фурье
Периодических сигналов в природе очень мало. В общем случае они непериодические. Но для их представления в пространстве частот нужны преобразования Фурье.
Спектр непериодического сигнала
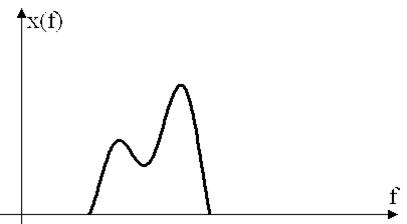
Сделаем из непериодической функции периодическую, для этого аналитически продолжим функцию. Это метод аналитического продолжения: размножение функции в обе стороны на бесконечном интервале.
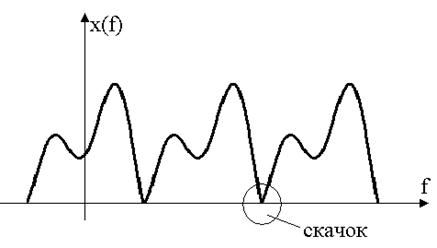
Теперь у нас периодическая функция → раскладываем в ряд Фурье → преобразование Фурье (за спектр при бесконечном разложении принимается спектр одной части (в пределе)).
Скачок – нарушение условий Дирихле. Спектр получить можно, но обратным преобразованием сигнал получить не сможем, возникнут искажения. Скачок (из-за разрыва на концах отрезка) дает паразитные явления → явления Гиббса.
Метод борьбы – использование «оконных функций». Чтобы убрать искажения надо умножить функцию на «окно». «Окно» сглаживает место стыковки.
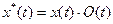 , где
, где 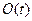 – функция окна.
– функция окна.
Используют различную форму окон – прямоугольное, треугольное и т.д. Требования, предъявляемые к функции окна – должны быть производные равны нулю.

 - прямое преобразование Фурье
- прямое преобразование Фурье
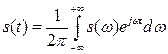 - обратное преобразование Фурье
- обратное преобразование Фурье
Если спектр симметричен, то сигнал действительный. Если спектр несимметричен, то сигнал мнимый.
Пример:Найти спектр одиночного импульса.
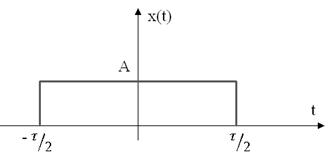
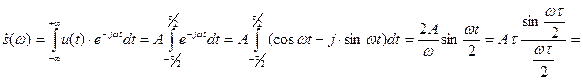

Cвойства Фурье:
- спектр комплексный
- ∆f* τ = const
- можно восстановить ф-цию времени по комплексному сигналу, но чтобы восстановленная ф-ция была действительной, её спектр должен быть симметричным.
Свертка двух функций во временной области: скалярное произведение функций, одна из которых сдвинута по времени.

Свертка двух функций в частотной области:

Если умножать две функции во временной области, то в частотной области их спектры свёртываются, и наоборот.
Корреляция двух функций:кросскорреляционная и автокорреляционная функции

Функция корреляции ищет сигнал, похожий на первоначальный. Она определяет максимальное статическое совпадение двух функций.
Свойство сдвига одной функции, относительно другой: Когда они наложены, то корреляция максимальна. Если находятся на расстоянии, то минимальна.

Лекция №3