Ряд Фурье.

Обобщенный ряд Фурье

Классическое представление сигнала – ряд Фурье. Он определён для периодических функций ( u(t)=u(t+T) ):

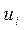– базисные вектора (синусы, косинусы), 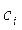- коэффициенты ряда Фурье.

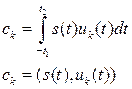
Еслинепрерывнаяфункция времени периодическая, то ее можно разложить в ряд Фурье, т. е. представить в виде суммы sin и cos:

,

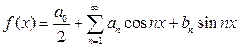где а₀ – постоянная составляющая.

Для тригонометрического ряда Фурье с периодом 2π:

 

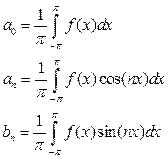
Если период T = 2l, то:

 

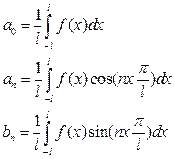
Любой сигнал имеет две абсолютно равноправные формы представления:

- в виде функции времени S(t) ( в пространстве времени t ≥ 0);

- в виде распределение сигнала по различным частотам S(f)(в пространстве частот).

Это называется дуальностью в представлении сигналов. Эти формы представления сигнала эквивалентны.

Спектральное представление сигнала:

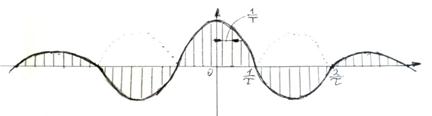
Сигналы бывают детерминированные и случайные. Для случайных сигналов определены только вероятностные характеристики (для них нет спектра), но зная вероятностные характеристики, можно определить энергетический спектр. Для детерминированных сигналов характерны определенные значения частоты, т.е. можно говорить о спектре.

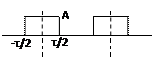Рассмотрим пример:

 

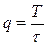- скважность, где Т-период импульса, а τ – длительность импульса.

, ,

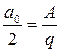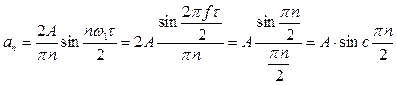где , n - № гармоники, ω₁ – главная гармоника.

Спектр линейчатый, так как функция периодическая.

 

Чем больше период, тем гуще спектр. Поэтому обычно T увеличивают, чтобы повысить точность разрешения по частоте. Чем короче импульс, тем более широкий диапазон частот занимает, т. е. для коротких импульсов спектр расширяется по частоте, а для длинных – сужается.

 

Чаще рисуют модуль:

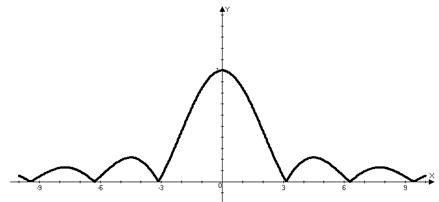
Принцип непределённости: Ограниченная по частоте функция бесконечна по длительности (и наоборот)

∆f – ширина спектра ∆f* τ = const

τ – длительность импульса