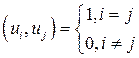Геометрические методы в теории сигналов.
Сигнал представляется точкой в пространстве сигналов. Сигнал образует бесконечномерное пространство.
Непрерывное пространство (вещественные числа), т. е. пространство непрерывных аналоговых сигналов – пр-во Гилберта. Дискретное пространство (целые числа), т. е. пространство цифровых сигналов – пространство Хэмминга.
Связь пространств – функция, связь пр-ва и функции – функционал, связь функций – оператор.
Расстояние между сигналами в пр-ве Хэмминга – это количество совпадающих битов двух цифровых сигналов, а в пр-ве Гилберта она вычисляется по т.Пифагора.
Пространство: вещественное или комплексное. Оно линейное (если два сигнала линейные, то и их сумма принадлежит линейному пр-ву).
В линейном пр-ве можно выделить координатный базис:

 .
.
Любой сигнал может быть разложен по этому базису: 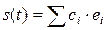 .
.
Длина вектора в этом пространстве – норма (положительное число) => пространство нормированное.
Норма:- вещественного числа: 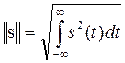
- комплексного числа: 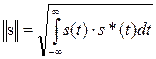
Энергия сигнала – квадрат его нормы: 
Метрическое пространство – линейное пр-во, если каждой паре элементов этого пр-ва сопоставлено некоторое неотрицательно число (метрика), т.е. расстояние между элементами. Расстояние определяется формулой:

Сигналы являются ортогональными, если их скалярное произведение равно нулю.

Если все вышеперечисленные условия (бесконечномерное, линейное, метрическое с ортонормированным базисом пр-во) выполняются, то пространство является Гилбертовым.
Виды базисов:
1) Гармонические (синус, косинус)
2) Ряд Фурье
3) Функции Уолша и т.д
Пример: Найти такое А, чтобы минимизировать расстояние между сигналами.
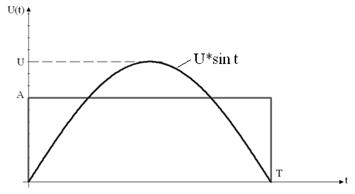
Решение:
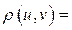
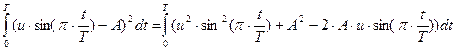
Так как в первом слагаемом отсутствует А, то его можно не рассматривать.
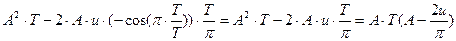
Чтобы расстояние было минимальным, необходимо найти минимум этой функции:

Лекция №2
Если есть система ортогональных функций в пр-ве Гилберта, то её можно разложить по базису.
Базис: