Точечные оценки

Статистические оценки могут быть точечными и интервальными.

Точечные оценки представляют собой число или точку на числовой оси. Чтобы оценка была близка к значению параметра , она должна обладать свойствами состоятельности, несмещенности и эффективности.

Определение. Оценка параметра называется состоятельной, если она сходится по вероятности к оцениваемому параметру, то есть для любого :

 

.

 

Поясним смысл этого равенства.

Пусть - очень малое положительное число. Тогда данное равенство означает, что чем больше объем выборки 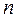, тем ближе оценка приближается к оцениваемому параметру .

Свойство состоятельности нужно проверять в первую очередь. Оно обязательно для любого правила оценивания. Несостоятельные оценки не используются.

 

Определение. Оценка параметра называется несмещенной, если , то есть математическое ожидание оценки равно оцениваемому параметру. Если, то оценка называется смещенной.

Это свойство оценки желательно, но не обязательно. Часто полученная оценка бывает смещенной, но ее можно поправить так, чтобы она стала несмещенной.

Иногда, оценка бывает асимптотически несмещенной ,

то есть .

Требования несмещенности особенно важно при малом числе опытов.

u/baza2/2064463037663.files/image295.gif" />является состоятельной, несмещенной и эффективной оценкой в классе линейных оценок;

- является состоятельной, смещенной оценкой ;

- является состоятельной, несмещенной оценкой ;

(при больших разница между и мала.

используется при малых выборках, обычно при ) ;

 

- относительная частота появления события в независимых испытаниях является состоятельной, несмещенной и эффективной оценкой, в классе линейных оценок, неизвестной вероятности (- вероятность появления события в каждом испытании);

 

- эмпирическая функция распределения выборки является состоятельной, несмещенной оценкой функции распределения случайной величины .

 

Для нахождения оценок неизвестных параметров используют различные методы. Наиболее распространенными являются: метод моментов, метод максимального правдоподобия (ММП), метод наименьших квадратов (МНК).