Для диагностики модели на гетероскедастичность ошибок применяется
а) Критерий Стьюдента.
б) Критерий Фишера.
в) Критерий Дарбина-Уотсона.
г) Критерий Пирсона.
д) Ни один из критериев, перечисленных в п.п. а-г.
Доверительная вероятность
а) Вероятность того, что фактическое и прогнозное значение результирующего показателя совпадут.
б) Вероятность того, что фактическое значение результирующего показателя не будет превосходить его прогнозное значение.
в) Вероятность получения недостоверного результата.
г) Вероятность того, что фактическое значение результирующего показателя попадет в рассчитанный прогнозный интервал.
д) Ни один из ответов в п.п. а-г не верен.
21. Тест Дарбина-Уотсона применяется для:
а) обнаружения недостающих регрессоров
б) выявления порядка автокорреляции
в) выявления автокорреляции в модели
22. Какая ошибка в спецификации имеет менее серьезные последствия:
а) включение в модель переменной, которой там быть не должно
б) исключение из модели значимой переменной
Каким образом можно обнаружить отрицательную автокорреляцию?
А) также как и положительную, только зона с критическим уровнем расположена симметрично справа от 2
б) также как и положительную, только зона с критическим уровнем расположена симметрично справа от 4
Какой показатель характеризует долю объясненной с помощью регрессии дисперсии в общей дисперсии зависимой переменной?
а)коэффициент детерминации.
б) коэффициент корреляции;
в) t-статистика;
г) F-статистика.
| Вопрос | ||||||||||||
| Ответ | а | а | г | в | г | а | б | в | а | д | в | а |
| Вопрос | ||||||||||||
| Ответ | а | б | б | б | д | а | д | г | в | а | б | а |
Тест 2
1. Наиболее наглядным видом выбора уравнения парной регрессии является:
а) аналитический;
б) графический;
в) экспериментальный (табличный).
2. Суть метода наименьших квадратов состоит в:
а) минимизации суммы остаточных величин;
б) минимизации дисперсии результативного признака;
в) минимизации суммы квадратов остаточных величин.
3. На основании наблюдений за 50 семьями построено уравнение регрессии 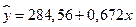 , где
, где  – потребление,
– потребление,  – доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?
– доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?
а) да;
б) нет;
в) ничего определенного сказать нельзя.
4. Качество модели из относительных отклонений по каждому наблюдению оценивает:
а) коэффициент детерминации  ;
;
б) F-критерий Фишера;
в) средняя ошибка аппроксимации  .
.
5. Классический метод к оцениванию параметров регрессии основан на:
а) методе наименьших квадратов:
б) методе максимального правдоподобия:
в) шаговом регрессионном анализе.
6. Какое уравнение регрессии нельзя свести к линейному виду:
а) 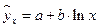 ;
;
б) 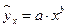 :
:
в) 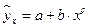 .
.
7. Параметр b в степенной модели является:
а) коэффициентом детерминации;
б) коэффициентом эластичности;
в) коэффициентом корреляции.
8. Добавление в уравнение множественной регрессии новой объясняющей переменной:
а) уменьшает значение коэффициента детерминации;
б) увеличивает значение коэффициента детерминации;
в) не оказывает никакого влияние на коэффициент детерминации.
9. Множественный коэффициент корреляции  . Определите, какой процент дисперсии зависимой переменной y объясняется влиянием факторов
. Определите, какой процент дисперсии зависимой переменной y объясняется влиянием факторов  и
и  :
:
а) 90%;
б) 81%;
в) 19%.
10. Стандартизованные коэффициенты регрессии  :
:
а) позволяют ранжировать факторы по силе их влияния на результат;
б) оценивают статистическую значимость факторов;
в) являются коэффициентами эластичности.
11. Частный F-критерий:
а) оценивает значимость уравнения регрессии в целом;
б) служит мерой для оценки включения фактора в модель;
в) ранжирует факторы по силе их влияния на результат.
12. Наибольшее распространение в эконометрических исследованиях получили:
а) системы независимых уравнений;
б) системы рекурсивных уравнений;
в) системы взаимозависимых уравнений.
13. Экзогенные переменные – это:
а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через x;
б) зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через y;
в) значения зависимых переменных за предшествующий период времени.
14. Для определения параметров структурную форму модели необходимо преобразовать в:
а) приведенную форму модели;
б) рекурсивную форму модели;
в) независимую форму модели.
15. Модель неидентифицируема, если:
а) число приведенных коэффициентов меньше числа структурных коэффициентов;
б) если число приведенных коэффициентов больше числа структурных коэффициентов;
в) если число параметров структурной модели равно числу параметров приведенной формы модели.
16. Уравнение идентифицируемо, если:
а) 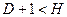 ;
;
б) 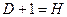 ;
;
в)  .
.
17. Уравнение сверхидентифицируемо, если:
а) 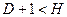 ;
;
б) 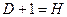 ;
;
в)  .
.
18. Для определения параметров сверхидентифицируемой модели:
а) применяется двухшаговый МНК;
б) применяется косвенный МНК;
б) ни один из существующих методов применить нельзя.
19. Аддитивная модель временного ряда имеет вид:
а) 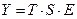 ;
;
б) 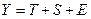 ;
;
в) 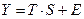 .
.
20. Коэффициент автокорреляции:
а) характеризует тесноту линейной связи текущего и предыдущего уровней ряда;
б) характеризует тесноту нелинейной связи текущего и предыдущего уровней ряда;
в) характеризует наличие или отсутствие тенденции.
21. Мультипликативная модель временного ряда строится, если:
а) значения сезонной компоненты предполагаются постоянными для различных циклов;
б) амплитуда сезонных колебаний возрастает или уменьшается;
в) отсутствует тенденция.
22. На основе поквартальных данных построена мультипликативная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 0,8 – I квартал, 1,2 – II квартал и 1,3 – III квартал. Значение сезонной компоненты за IV квартал есть:
а) 0,7;
б) 1,7;
в) 0,9.
23. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:
а) не менее 5 наблюдений;
б) не менее 7 наблюдений;
в) не менее 10 наблюдений.
24. Для оценки значимости коэффициентов регрессии рассчитывают:
а) F-критерий Фишера;
б) t-критерий Стьюдента;
в) коэффициент детерминации 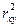 .
.
25. Коэффициент корреляции 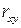 может принимать значения:
может принимать значения:
а) от –1 до 1;
б) от 0 до 1;
в) любые.
| Вопрос | |||||||||||||
| Ответ | б | в | а | в | а | в | б | б | б | а, б | б, в | в | а |
| Вопрос | |||||||||||||
| Ответ | а | а | б | в | а | б | а | б | а | б | б | а |
Тест 3
1. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:
а) не менее 5 наблюдений;
б) не менее 7 наблюдений;
в) не менее 10 наблюдений.
2. Коэффициент линейного парного уравнения регрессии:
return false">ссылка скрытаа) показывает среднее изменение результата с изменением фактора на одну единицу;
б) оценивает статистическую значимость уравнения регрессии;
в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.
3. Суть коэффициента детерминации 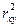 состоит в следующем:
состоит в следующем:
а) оценивает качество модели из относительных отклонений по каждому наблюдению;
б) характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака;
в) характеризует долю дисперсии y, вызванную влиянием не учтенных в модели факторов.
4. Значимость уравнения регрессии в целом оценивает:
а) F-критерий Фишера;
б) t-критерий Стьюдента;
в) коэффициент детерминации 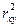 .
.
5. Остаточная сумма квадратов равна нулю:
а) когда правильно подобрана регрессионная модель;
б) когда между признаками существует точная функциональная связь;
в) никогда.
6. Для оценки значимости коэффициентов регрессии рассчитывают:
а) F-критерий Фишера;
б) t-критерий Стьюдента;
в) коэффициент детерминации 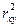 .
.
7. Какое из уравнений является степенным:
а) 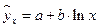 ;
;
б) 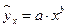 :
:
в) 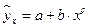 .
.
8. Коэффициент корреляции 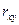 может принимать значения:
может принимать значения:
а) от –1 до 1;
б) от 0 до 1;
в) любые.
9. Какое из следующих уравнений нелинейно по оцениваемым параметрам:
а) 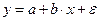 ;
;
б)  ;
;
в) 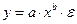 .
.
10. Для построения модели линейной множественной регрессии вида 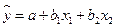 необходимое количество наблюдений должно быть не менее:
необходимое количество наблюдений должно быть не менее:
а) 2;
б) 7;
в) 14.
11. Частные коэффициенты корреляции:
а) характеризуют тесноту связи рассматриваемого набора факторов с исследуемым признаком;
б) содержат поправку на число степеней свободы и не допускают преувеличения тесноты связи;
в) характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
12. При наличии гетероскедастичности следует применять:
а) обычный МНК;
б) обобщенный МНК;
в) метод максимального правдоподобия.
13. Если качественный фактор имеет три градации, то необходимое число фиктивных переменных:
а) 4;
б) 3;
в) 2.
14. Эндогенные переменные – это:
а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через x;
б) зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через y;
в) значения зависимых переменных за предшествующий период времени.
15. Лаговые переменные – это:
а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через x;
б) зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через y;
в) значения зависимых переменных за предшествующий период времени.
16. Модель идентифицируема, если:
а) число приведенных коэффициентов меньше числа структурных коэффициентов;
б) если число приведенных коэффициентов больше числа структурных коэффициентов;
в) если число параметров структурной модели равно числу параметров приведенной формы модели.
17. Модель сверхидентифицируема, если:
а) число приведенных коэффициентов меньше числа структурных коэффициентов;
б) если число приведенных коэффициентов больше числа структурных коэффициентов;
в) если число параметров структурной модели равно числу параметров приведенной формы модели.
18. Уравнение неидентифицируемо, если:
а) 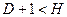 ;
;
б) 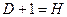 ;
;
в)  .
.
19. Уравнение неидентифицируемо, если:
а) 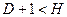 ;
;
б) 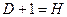 ;
;
в)  .
.
20. Для определения параметров неидентифицируемой модели:
а) применяется двухшаговый МНК;
б) применяется косвенный МНК;
в) ни один из существующих методов применить нельзя.
21. Мультипликативная модель временного ряда имеет вид:
а) 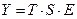 ;
;
б) 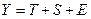 ;
;
в) 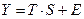 .
.
22. Аддитивная модель временного ряда строится, если:
а) значения сезонной компоненты предполагаются постоянными для различных циклов;
б) амплитуда сезонных колебаний возрастает или уменьшается;
в) отсутствует тенденция.
23. На основе поквартальных данных построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 7 – I квартал, 9 – II квартал и –11 – III квартал. Значение сезонной компоненты за IV квартал есть:
а) 5;
б) –4;
в) –5.
24. Критерий Дарбина-Уотсона применяется для:
а) определения автокорреляции в остатках;
б) определения наличия сезонных колебаний;
в) для оценки существенности построенной модели.
25. Качество модели из относительных отклонений по каждому наблюдению оценивает:
а) коэффициент детерминации 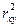 ;
;
б) F-критерий Фишера;
в) средняя ошибка аппроксимации  .
.
| Вопрос | |||||||||||||
| Ответ | б | а | б | а | б | б | б | а | в | в | в | б | в |
| Вопрос | |||||||||||||
| Ответ | б | в | б | б | а | а | в | а | а | в | а | в |
Раздел 7. Список рекомендуемой литературы