Выборочное среднее квадратическое отклонение
Выборочное среднее. Выборочная дисперсия.
Числовые характеристики выборки
В теории вероятностей определили числовые характеристики для случайных величин, с помощью которых можно сравнивать однотипные случайные величины. Аналогично можно определить ряд числовых характеристик и для выборки. Поскольку эти характеристики вычисляются по статистическим данным (по данным, полученным в результате наблюдений), их называют статистическими характеристиками.
Пусть дано статистическое распределение выборки объема 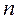 :
:
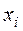
| 
| 
| 
| 
| 
| 
|
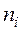
| 
| 
| 
| 
| 
| 
|
где 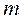 - число вариантов.
- число вариантов.
Определение. Выборочным средним  называется среднее арифметическое всех значений выборки:
называется среднее арифметическое всех значений выборки:
 .
.
Выборочное среднее можно записать и так:  ,
,
где 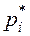 - частость.
- частость.
В случае интервального статистического ряда в качестве 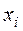 берут середины интервалов, а
берут середины интервалов, а 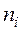 - соответствующие им частоты.
- соответствующие им частоты.
Определение. Выборочной дисперсией называется среднее арифметическое квадратов отклонений значений выборки от выборочного среднего
называется среднее арифметическое квадратов отклонений значений выборки от выборочного среднего  :
:
 или
или  .
.
Выборочное среднее квадратическое выборки определяется формулой:
 .
.
Особенность  состоит в том, что оно измеряется в тех же единицах, что и данные выборки.
состоит в том, что оно измеряется в тех же единицах, что и данные выборки.
Если объем выборки мал ( ), то пользуются исправленной выборочной дисперсией:
), то пользуются исправленной выборочной дисперсией:
 .
.
Величина  называется исправленным средним квадратическим отклонением.
называется исправленным средним квадратическим отклонением.