Эмпирическая плотность распределения

Пример 2.

Построить эмпирическую функцию и ее график по данным табл.1

¦

 

 

 

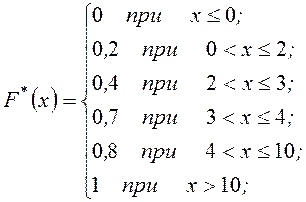
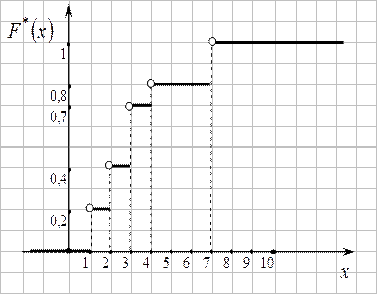
Рис. 1

˜

 

 

Для интегральной функции распределения 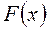справедливо приближенное равенство: ,

где - дифференциальная функция распределения (функция плотности вероятности).

Потому естественно выборочным аналогом функции считать функцию:

,

где 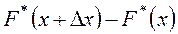- частость попадания наблюдаемых значений случайной величины 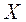в интервал 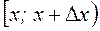. Таким образом, значение 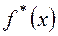характеризует плотность частости на этом интервале.

 

Пусть наблюдаемые значения непрерывной случайной величины представлены в виде интервального вариационного ряда.

Полагая, что 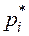- частость попадания наблюдаемых значений в интервал

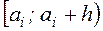, где - длина частичного интервала, выборочную функцию плотности 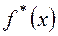можно задать соотношением

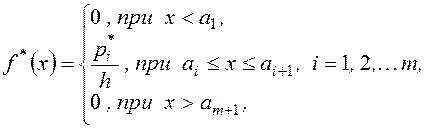
где 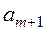- конец последнего - го интервала.

Так как функция 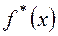является аналогом распределения плотности случайной величины, площадь область под графиком этой функции равна 1.