Примеры экономических задач оптимизации и управления

Пример 1

Некоторый регион производит n-продуктов только своими силами и для населения своего региона. Предполагается, что технологический процесс отработан, спрос на товары изучен. Необходимо определить годовой объем выпуска продуктов, с учетом того, что данный объем обеспечит и произвольное потребление.

Пусть C_i – спрос населения на i-й продукт. Тогда, вектор спроса C = (C₁,…,C_n).

Пусть a_ij – количество i-го продукта, которое необходимо для выпуска единицы j-го продукта, i = 1,…,n; j = 1,…,n.

Пусть x_i – объем выпуска i-го продукта. Вектор выпуска обозначим:

X = (x₁,…,x_n).

Вектор X разделяется на две части:

C – конечное потребление,

X - C – воспроизводство.

Сумма показывает ту величину i-го товара, какая нужна для всего выпуска.

Если это равенство расписать в виде системы n-линейных уравнений:

Это можно обозначить как систему, которую можно решить как уравнение относительно x₁, x₂,…,x_n. Можно выбрать нахождение определителя, составленного из коэффициентов при неизвестных A = a_ij.

Получается квадратная матрица размера n×n, которая носит название технологической, поэтому модель может быть записана в виде:

X – C = AX

Данная модель является классической моделью «Затраты-выпуск».

Пример 2

Нефтеперерабатывающий завод располагает двумя сортами нефти. Сорт А – 10 единиц, В – 15 единиц. При переработке из нефти получают два материала: бензин (Б) и мазут (М). Имеется три варианта технологического процесса переработки:

I. 1А + 2В = 3Б + 2М

II. 1А + 1В = 1Б + 5М

III. 2А + 2В = 1Б + 2М

Цена Б 10$ за единицу, М – 1$. Определить наиболее выгодное сочетание технологического процесса имеющегося количества нефти.

Введем обозначения:

x_i – количество использования i-го технологического процесса (1-3).

Для вектора x_i выручка завода равна:

32x₁ + 15x₂ + 12x₃ ($).

Учет запаса нефти ведет к выполнению следующих условий:

· для сорта А x₁ + 2x₂ + 2x₃ ≤ 10

· для сорта В 2x₁ + x₂ + 2x₃ ≤ 15

Коэффициенты 1, 2, 2 – это нормы расхода сорта А; 2, 1, 2 – нормы расхода В.

Математическая модель заключается в следующем: найти такой вектор x = (x₁, x₂, x₃), чтобы максимизировать выручку или функцию f(x).

f(x) = 32x₁ + 15x₂ + 12x₃.

при выполнении условий для сорта А и В, x₁, x₂, x₃ – целые положительные числа.

При данных условиях мы получили задачу линейного программирования, то есть задачу максимизации целевой функции: f(x)→max при заданных условиях.

Данная модель является примером оптимизационной модели детерминированного типас определенными элементами.

Пример 3

Инвестор определяет наилучший выбор из акций, облигаций и других ценных бумаг для их приобретения на некоторую сумму с целью получения определенной прибыли с линейным риском для себя. Прибыль на каждый доллар, вложенный в ценные бумаги j-го вида, характеризуется двумя показателями:

1) ожидаемая прибыль

2) фактическая прибыль

Для инвестора желательно, чтобы ожидаемая прибыль на 1$ вложения для всего набора ценных бумаг была бы не ниже заданной величины.

Известные параметры:

n – число разновидностей ценных бумаг,

a_i – фактическая прибыль i-го вида ценных бумаг,

d_i – ожидаемая прибыль.

Неизвестная величина - это средства, которые выделяются для приобретения ценных бумаг i-ого вида. Вся инвестированная сумма выражается как сумма . Для упрощения модели можно ввести обозначения:

.

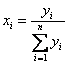Откуда видно, что - это доля всех средств, которые выделяются для приобретения ценных бумаг j-ого вида.

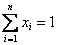
Данное соотношение определяет основную цель инвестора достижение определенного уровня прибыли с минимальным риском.

Риск – это мера отклонения фактической прибыли от ожидаемой, поэтому риск может отождествляться с ковариацией:

.

Тогда математическая модель может быть представлена в виде минимизации следующей суммы.

При ограничениях

.

Данная модель носит название модели Марковица для оптимизации структуры портфеля ценных бумаг. Данная модель – это модель стохастического типа или модель с элементами случайности.

Пример 4

На базе торговой организации имеется n типов одного из товаров ассортиментного минимума. В магазин должен быть ввезен только один из типов данного товара. Требуется выбрать тот тип товара, который целесообразно завести в магазин. Если товар типа j будет пользоваться спросом, то магазин от его реализации получит прибыль P_j, если убыток - Q_j.

В данной задаче лицо, принимающее решение, - это магазин. Получение максимальной прибыли зависит не только от его решения, но и от того, будет ли данный товар пользоваться спросом. Полагается, что по какой-то причине у магазина нет возможности изучить спрос. Поэтому население выбирает по предпочтению. Наихудший вариант: завезенный товар не пользуется спросом. Поэтому, чтобы учесть различные ситуации, магазину нужно считать население своим противником, который пытается преследовать противоположную цель, т. е. минимизировать прибыль магазина.

Имеем задачу принятия решения с двумя участниками с противоположными целями. Для этого составляется таблица с n строками и m столбцами:

строки – выбор магазина,

столбцы – выбор населения.

Ячейка (i, j) соответствует той ситуации, когда магазин выбирает j-ый тип товара, а население выбирает j-ый тип товара. В соответствующую колонку записывают числовую оценку (прибыль или убыток) к данной ситуации.

Получаем матрицу , на главной диагонали которой стоит уровень прибыли P_j, остальные элементы – это убыток Q_j.

Сокращенно составляется матрица из уровней P и Q.

P	Q	Q	Q
Q	P	Q	Q
Q	Q	P	Q
Q	Q	Q	P

Решение данной матрицы является примером игровой модели принятия решения.