Продукционные модели представления знаний.

Фразеология русского языка

Калькирование и полукалькирование.

Освоение заимствованных слов.

Заимствованные слова.

Как определить заимствованные слова:

Фонетическое оформление

1) Слова на а-, ф-, э-

2) Слова с сочетаниями гласных ау, иэ, согласных к, гз, кз, шт

3) Слова с сочетаниями ге, ке, фе, ант, аж, ив, ист, изм, ор, ори, ура

Семантическое оформление:

1) Спортивные термины (чаще всего) – англ.

2) Названия рыб – финск.

3) Морские термины – голланд.

4) Мода, парфюмерия – франц.

5) Музыканты – итальянск.

 

Фонетическое освоение заимствованных слов – при заимствовании звуки из языка-источника могут изменяться, приспосабливаясь к фонетике заимствующего языка

Виды: 1) Пропуск звуков (анг. Cakes – кекс, греч. Thearton – театр)

2) Вставка звука (Sitc – синтез)

Морфологическое освоение – меняется морфологическое значение – le vase (м.р.) – ваза (ж.р.)

 

 

Калька – перевод частей заимствованных слов

Полукалька – полуперевод – полузаимствование (пить на брудершавт)

 

 

Фразеологизм – относительно устойчивая, воспроизводимая в готовом виде единица языка, состоящая из 2 или более ударных компонентов, словного характера, фиксированная по своему значению, составу и характеристике.

Виды признаков фразеологизмов:

1) Релевантные (обязательные): воспроизводимость в готовом виде, биакцентность (2 или более акцентов (ударений)), фиксированность по своему значению

2) Факультативные (необязательные): относительная устойчивость (морфологическая, синтаксическая и лексическая), образность (при помощи сравнений – как селедка в корсете; метафоры, метонимии, эвфемизмов, каламбуров – лить воду на мельницу) и необразность (безобразность) (тавтология – ходуном ходить; аналитическая), имплецидные (имеют свойство сокращать количество компонентов состава) и эксплецидность (расширение компонентов состава фразеологизмов), симметрия/ассиметрия (форма и содержание совпадает/ не совпадает; приказал долго жить – ассиметрия)

Источники русской фразеологии:

1. Исторические события и факты, лежащие в основе фразеологизма – Казанская сирота, кричать во всю Ивановскую

2. Традиции алфавита и книжного дела – ни азов не знают

3. На основе традиций и обычаев – хлеб-соль

4. Сказки и художественная литература – молочные реки и кисельные берега, небо в алмазах (Чехов «Дядя Ваня»)

5. Профессиональная деятельность – довести до белого каления

6. Игры – играть в бирюльки

7. Религия – Ради Бога, ищите и обретете

8. Заимствования – Альма-матер (полукалька), желтая пресса (Yellow press), золотой парашют (деньги при увольнении) (калька)

 

Продукционная модель является одной из самых распространенных. Представление знаний с помощью правил-продукций имеет в некоторых отношениях сходство с правилами вывода логических моделей. Это позволяет с помощью продукций выполнять эффективный вывод и, кроме того, благодаря естественной аналогии процессу рассуждений человека, данные модели нагляднее отражают знания.

Во многих случаях правило-продукцию записывают в обобщенной форме R_nj: (Pr, Bc, A → B, Ac), где:

R_nj - идентификатор j-той продукции в n-ном наборе продукций;

Pr – приоритет правила продукции;

Bc – предусловие применимости ядра продукции, представляющее предикат, при выполнении которого активизируется ядро продукции;

Aс – постусловие продукции, определяющее действие и процедуры, которые необходимо выполнить после выполнения ядра продукции.

В общем случае, продукционная система включает следующие компоненты:

1. Базу продукционных правил.

2. Базу данных (рабочую память).

3. Интерпретатор.

Множество продукционных правил образует базу правил, каждое из которых представляет обособленный фрагмент знаний о решаемой проблеме. Психологи называют такие фрагменты чанками. Считается, что чанк – объективно существующая единица знаний, выделяемая человеком в процессе познания окружающего мира.

Предпосылка, или условие правила, часто рассматривается как образец. Образец – некоторая информационная структура, определяющая обобщенную ситуацию (условие, состояние и т.п.), окружающей действительности, при которой активизируется правило.

Рабочая память (глобальная база данных) отражает конкретные ситуации (состояния, условия и т.д.), возникающие во внешней среде.

Информационная структура, представляющая конкретную ситуацию внешней среды в рабочей памяти, называется образом.

Интерпретатор реализует логический вывод. Процесс выводы является циклическим и называется поиском по образцу. В упрощенной форме он выглядит следующим образом:

Текущее состояние моделируемой предметной области отражается в рабочей памяти в виде совокупности образов, каждый из которых представляется посредством фактов. Рабочая память инициализируется фактами, описывающими задачу. Затем выбираются те правила, для которых образцы, представляемые предпосылками правил, сопоставимы с образами в рабочей памяти.

Данные правила образуют конфликтное множество. Все правила, входящие в конфликтное множество, могут быть активизированы. В соответствии с выбранным механизмом разрешения конфликта, активизируется одно из правил.

Выполнение действия, содержащегося в заключении правила, приводит к изменению состояния рабочей памяти. В дальнейшем цикл управления выводом повторяется. Указанный процесс завершается, когда не окажется правил, предпосылки которых сопоставимы с образами рабочей памяти.

Таким образом, процесс вывода, основанный на поиске по образцу, состоит из 4 шагов:

- 1 шаг – выбор образа,

- 2 шаг – сопоставление образа с образцом и формирование конфликтного набора правил,

- 3 шаг – разрешение конфликтов,

- 4 шаг - выполнение правила.

Рассмотрим пример функционирования продукционной системы на примере сортировки строки. Правила сортировки имеет следующий вид:

1. ва→ав 2. са→ас 3.св→вс

Если образец сопоставим с частью сортируемой строки, то правило активизируется. В результате этого подстрока, которая совпала с условием правила, замещается подстрокой из заключительной части правила.

Рассматривая исходную и отсортированную строки как начальное и конечное состояние задачи, а продукционные правила как операторы, преобразующие одно состояние в другое, приходим к выводу, что поиск решения в продукционных системах соответствует поиску в пространстве состояний.

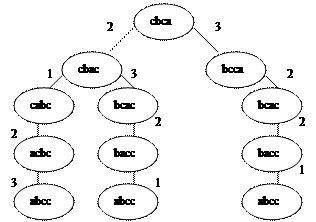Для этого примера дерево решения примет следующий вид:

 

Вершины дерева соответствуют промежуточным состояниям строки, а ребра – продукциям.

Широкое применение продукционных моделей определяется следующими основными достоинствами:

- универсальностью – практически любая область знаний может быть представлена в продукционной форме,

- модульностью – каждая продукция представляет собой элемент знаний о предметной области, удаление одних и добавление других продукций выполняется независимо,

- декларативностью – продукции определяют ситуации предметной области, а не механизм управления,

- естественностью процесса вывода заключений, который во многом аналогичен процессу рассуждений эксперта,

- асинхронностью и естественным параллелизмом, который делает их весьма перспективными для реализации на параллельных ЭВМ.

Однако продукционные модели не свободны от недостатков:

1. Процесс вывода имеет низкую эффективность, так как при большом числе продукций значительная часть времени затрачивается на непроизводительную проверку условий применения правил.

2. Проверка непротиворечивости системы продукций становится весьма сложной из-за недетерминированности выбора выполняемой продукции из конфликтного множества.

 

Управление выводом в продукционных системах.

В ходе решения задачи машина вывода, или интерпретатор, выполняет 2 задачи – собственно логический вывод и управление выводом.

Логический вывод в продукционных системах реализуется на основе процедуры поиска по образцу.

Управление выводом в продукционных системах предполагает решение двух вопросов:

1. С чего следует начинать процесс вывода?

2. Как поступить, если на некотором шаге вывода возможен выбор различных вариантов его продолжения?

Ответ на первый вопрос приводит к прямой и обратной цепочке рассуждений, а на второй вопрос – к механизмам разрешения конфликтов в продукционных системах.

Прямой вывод начинается с задания исходных данных решаемой задачи, которые фиксируются в виде фактов в рабочей памяти системы.

Правила, применяемые к исходным данным, обеспечивают генерацию новых фактов, добавляемых в рабочую память. Процесс продолжается, пока не будет получено целевое состояние рабочей памяти.

Рассмотрим пример поиска управляемого данными на множестве продукций, записанных в виде логических формул. На каждом шаге работы машины вывода применяется простая стратегия разрешения конфликтов: активизируется последнее из успешно сопоставленных правил.

Порядок сопоставления правил соответствует их номерам.

1) G∩H→C 2)I∩K→D 3)L∩M→E 4)N→F 5)O→F 6)C→A 7)D→A 8)E→B 9)F→B 10)A→goal 11)B→goal

Исходные данные START={L,M,N}

N шага	Рабочая память	Конфликтное множество	Активизируемое правило
	L,M,N	-	-
	L,M,N	3,4
	L,M,N,F	3,9
	L,M,N,F,B	3,11
	L,M,N,F,B,Goal		Остановка

Выбранная стратегия активизации последнего правила, добавленного в конфликтное множество, соответствует поиску в глубину. Именно эта стратегия наиболее часто применяется в экспертных системах продукционного типа, так как она соответствует процессу рассуждения эксперта при решении той или иной задачи.

Поведение системы для пользователя выглядит довольно логичным. Он видит, что система стремится свести каждую цель к подцели.

Кроме прямого вывода, в продукционных системах широко применяется и обратный вывод, то есть вывод, управляемый целевыми условиями. Такой вывод начинается с целевого утверждения, которое фиксируется в рабочей памяти.

Затем отыскивается правило-продукция, заключение которого сопоставимо с целью. Условия данного правила помещаются в рабочую память и становятся новой подцелью. Процесс повторяется до тех пор, пока в рабочей памяти не будут найдены факты, подтверждающие целевое утверждение.

Проиллюстрируем обратный вывод на множестве продукций предыдущего примера. Процесс вывода начинается с того, что в рабочую память помещается целевое утверждение Goal, истинность которого необходимо подтвердить или опровергнуть, а также множество исходных фактов {L,M,N}, которые считаются истинными утверждениями.

Удобно рассматривать переменные правил как многозначные объекты, характеризуемые тремя возможными значениями: «не определено», «истина», «ложь». В этом случае начальное значение переменной Goal не определено, а факты L,M,N имеют значение «истина».

№ шага	Рабочая память	Конфликтное множество	Актив. Правило
	Goal, L*, M*, N*	10, 11
	Goal, A, L*, M*, N*	11, 6, 7
	Goal, A, B, L*, M*, N*	6,7,8,9
	Goal, A, B, C, L*, M*, N*	7,8,9,1
	Goal, A, B, C, D, L*, M*, N*	8,9,1,2
	Goal, A, B, C, D, E, L*, M*, N*	9,1,2,3
	Goal, A, B, C, D, E, F,L*, M*, N*	1,2,3,4,5
	Goal, A, B, C, D, E, F, G, H, L*, M*, N*	2,3,4,5
	Goal, A, B, C, D, E, F, G, H, I, K, L*, M*, N*	3,4,5
	Goal*, A, B*, C, D, E*, F, G, H, I, K, L*, M*, N*	3,4	Остановка

Вывод начинается с целевого утверждения Goal, которое рассматривается как текущая подцель. Все продукционные правила, заключения которых сопоставимы с текущей подцелью, добавляются в конфликтное множество правил.

На каждом шаге активизируется первое правило конфликтного множества. Посылки данного правила добавляются в рабочую память и на следующем шаге выступают в качестве новой подцели системы.

Такая стратегия разрешения конфликтов соответствует поиску в ширину.

Сравнивая прямой и обратный вывод, можно заключить, что прямой вывод имеет более широкую область применения. Объясняется это тем, что обратный вывод будет эффективен в том случае, если решаемая проблема характеризуется немногими четко определенными целевыми состояниями.

Когда количество целевых состояний велико или их определение является частью самой проблемы, то обратный вывод мало пригоден. Подобные ситуации встречаются, например, при решении задач планирования, где план является одновременно и целевым состоянием, и искомым решением, в медицинских экспертных системах при назначении методики решения и других.