Основы оптимального решения сетевых задач

Неклассифицируемые методы оптимизации

Пример

g(x) = 0.25x⁴ + x ^{− 1.5} + 2x⁹.

 

4.4. Выпуклое программирование. Целевая функция - выпуклая и ограниченная, должна быть в форме выпуклой области.

4.5. Нелинейное программирование. Целевая функция от многих переменных является нелинейной и (или) допустимая область определяется нелинейными ограничениями. Иногда методами нелинейного программирования решаются задачи 4.2 - 4.4.

4.5.1. Прямые методы поиска экстремума одно-экстремальной целевой функции без ограничений.

4.5.2. Прямые методы поиска экстремума функции многих переменных с параметрическими ограничениями.

4.5.3. Прямые методы условной оптимизации при произвольных ограничениях.

4.5.4. Методы поиска экстремума функции по вычисляемым значениям ее производной.

4.5.4.1. Методы первой производной.

4.5.4.2. Методы второй производной.

4.6. Стохастическое программирование. Изучает методы выбора оптимальных решений в ситуациях, характеризуемых случайными величинами.

4.7. Динамическое программирование. Изучает многошаговые процессы поиска экстремума не в виде одного значения, а в виде функции изменения значения во времени или пространстве, т.е. оптимальное решение может быть получено в форме функции (политики) управления системой с минимумом затрат на перевод системы из одного состояния в другое.

Не классифицируемые (комбинированные или уникальные) методы оптимизации, которые трудно отнести к какому-либо разделу данной классификации.

Примеры не классифицируемых методов:

1) методы оптимального решения сетевых задач позволяют эффективно решать задачи, которые решались ранее методами линейного или динамического программирования;

2) численные методы решения задач вариационного исчисления.

Методы решения задач оптимизации на графах являются мощным математическим средством, с помощью которого могут быть сформулированы и решены многие технологические, конструкторские, проектные и экономические задачи. Наглядность и логическая обоснованность этих методов, естественный подход к решению поставленных задач, малые вычислительные затраты как по времени, так и по памяти при той же размерности, позволили отказаться от традиционного использования алгоритмов линейного и целочисленного программирования для множества приложений. Некоторые из задач могут быть успешно решены с использованием динамического программирования.

Преимущества алгоритмов оптимизации на графах состоят в следующем.

Преимущество 1. Сетевые модели в форме графов могут точно описывать многие реально существующие системы и могут быть использованы на практике при проектировании больших оросительных систем, вычислительных комплексов, транспортных систем, систем связи; при решении практических задач, связанных со складированием, распределением товаров, календарным планированием выполняемых работ (сетевые графики проекта), заменой оборудования, контролем издержек, перевозками, работы систем массового обслуживания, обеспечением ритмичности производственного процесса, управление запасами, распределение рабочей силы, при реализации операционных систем, при реализации СУБД с большими объемами информации, планирование семейного бюджета и т.п.

Преимущество 2. Сетевая модель определенного вида требует применения специализированного вида оптимизации. Вообще, конкретный метод оптимизации на графах уже ориентирован на определенную модель, что облегчает выбор метода.

Преимущество 3. Сетевые модели более понятны практикам, чем иные методы исследования операций. Практику легче понять сетевые диаграммы, чем абстрактные формулы.

Преимущество 4. По сравнению с другими методами оптимизации, сетевые алгоритмы нередко позволяют решать задачи со значительно большим числом переменных и ограничений применяемых ресурсов оперативной памяти и машинного времени.

Методы оптимизации на графах часто относят к методам сетевого анализа. Эти методы в значительной степени основаны на теории графов. В них используются элементы теории динамического, линейного программирования, матричной алгебры. Сеть состоит из множества узлов и дуг, соединяющих узлы. Узлы иногда называют вершинами или точками. Дуги - ребрами, звеньями, линиями или ветвями. Чтобы упростить рассмотрение задачи, узлы нумеруют в определенном порядке. Дуги могут иметь или не иметь направления.

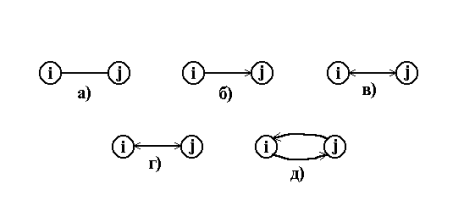Рис. 4.1. Классификация дуг: а) неориентированная дуга между узлами i и j; б) ориентированная дуга от узла i к узлу j; в) биориентированная дуга к узлам i и j; г) биориентированная дуга заменена двумя ориентированными дугами.

 

Иногда сетью описывается множество маршрутов продвижения. Для этих случаев применимы следующие термины.

Цепью из узла i в узел j называется последовательность дуг и узлов, в которой конечный узел каждой дуги является начальным узлом следующей дуги (исключая первый и последний узлы последовательности). Следовательно, каждая дуга в такой последовательности ориентированна по направлению от узла i к узлу j. Путь, в отличие от цепи, допускает прохождение вдоль дуг навстречу их ориентации.

Неориентированная цепь - это цепь у которой имеется хотя бы одна из дуг без ориентации.

Циклом называется конечный путь, начальный и конечный узлы которого совпадают.

Контуром называется конечная цепь, начальный и конечный узлы которой совпадают.

Сети могут быть бесконтурными и ациклическими (без циклов).

Связной сетью называется такая сеть, что для любых двух различных узлов существует по крайней мере один соединяющий их путь или соединяющая их цепь.

Остовное дерево сети - это сеть, являющаяся связным подмножеством всех узлов исходной ориентированной или неориентированной сети, но не содержащая циклов. Дерево получается из исходной сети отбрасыванием "лишних" дуг, то есть оно содержит n узлов, как у исходной сети и (n-1) дугу.

Далее приведен список наиболее распространенных алгоритмов оптимального решения сетевых задач. Модификации этих алгоритмов различаются достижением увеличения значения у одного из показателей: размерности решаемых задач, быстродействия работы, объема используемой оперативной памяти. Все они были реализованы автором данной книги в виде программ. Целесообразно включить данные алгоритмы в электронную таблицу, поскольку интерфейс электронных таблиц является удобным для этих методов.

Список алгоритмов представляет собой фонд методов, необходимый для определения способа решения конкретных задач.

Алгоритм Дейкстры нахождения кратчайшего пути (оптимизирован по быстроте счета).

Вводимая информация: число узлов в сети, число дуг в сети, описания дуг. Описание дуги содержит: номер начального узла дуги, номер конечного узла дуги, затраты вдоль дуги.

Выводимая информация: таблица наименьших затрат от всех узлов до конечного узла; значение наименьших затрат от первого узла до конечного; таблица характеристик дуг вдоль цепи с наименьшими затратами, которые включают начальный и конечный узлы дуги и затраты вдоль дуги.

Если из начального узла сети нет ни одной цепи до конечного узла, выдается сообщение о разрывности цепи.

Алгоритм Флойда нахождения цепей с наименьшими затратами между всеми парами узлов ориентированной цепи.

Вводимая информация та же, что у алгоритма Дейкстры.

Результат: реализация алгоритма Дейкстры для всех пар. Алгоритм двойного поиска нахождения кратчайшей и минимально худших резервных цепей от заданного начального узла до заданного конечного узла.

Вводимая информация та же, что у двух предшествующих методов, но дополнительно указывается число резервных цепей.

В результате выдается самый кратчайший путь и возможные другие цепи в порядке убывания качества.

Данный алгоритм используется для страховки перемещений.

Поедающий алгоритм построения кратчайшего остовного дерева неориентированной сети.

Физический смысл задачи: пусть в узле 1 находится районная электростанция, остальным узлам соответствуют села, требуется спроектировать схему электроснабжения с минимальной протяженностью линий электропередачи.

Вводимая информация: число узлов, число дуг, описания дуг.

Описание дуги: начальный узел дуги, конечный узел дуги, затраты вдоль дуги. Узел 1 является корневым для ствола (начальным узлом).

В результате работы этого алгоритма будет получено описание схемы электроснабжения с наикратчайшей протяженностью линий электропередачи.

Алгоритм нахождения кратчайшего контура, соединяющего все узлы ориентированной сети (алгоритм ветвей и границ Литтла).

Назначение - решение задачи коммивояжера, который должен по кратчайшему пути побывать во всех узлах сети и вернуться в начальный.

Алгоритм расстановок пометок Форда и Фалкерсона осуществляет поиск таких потоков по дугам с ограниченной пропускной способностью ориентированной сети, что результирующий поток из главного источника в главный сток является максимальным.

Вводимая информация: число узлов, число дуг, описания дуг. Описание дуги: номер узла начала и конца дуги, максимальная пропускная способность дуги.

Алгоритм Гомори-Ху нахождения цепей с максимальной пропускной способностью для каждой пары узлов источник-сток в ориентированной многополюсной цепи.

Вводимая информация та же, что и у метода Форда-Фалкерсона, но метод сразу находит пропускные способности между всеми парами узлов.

Обобщенный алгоритм дефекта нахождения оптимальных решений в различных потоковых задачах с ориентированными сетями и дугами с ограниченными пропускными способностями.

При помощи данного алгоритма могут быть решены следующие задачи: транспортные, задачи о назначениях, о максимальном потоке, о кратчайшем дереве, о перевозках, о максимальном потоке минимальной стоимости, о кратчайшей цепи, задачи производственного планирования.

Для решения многих задач необходимо искусственно подобрать или пропускные способности или включать новые дуги.

Вводимая информация: число дуг, число ветвей, описание каждой дуги сети, которая состоит из номера начального узла дуги, номера конечного узла дуги, верхней границы потока по дуге, нижней границы потока по дуге, стоимости прохождения единицы потока из начального узла дуги в конечный узел.

Узел 1 считается начальным, узел с максимальным номером - конечным.

Алгоритм Йенсена-Бомика нахождения потока минимальной стоимости на обобщенных сетях с выигрышами и проигрышами.

Здесь каждой дуге предписаны следующие числа: минимальное допустимое значение потока по данной дуге; максимальное допустимое значение потока по данной дуге; стоимость перемещения единицы потока по дуге, коэффициент показывающий, какая часть потока начала дуги достигает конца дуги. Если этот коэффициент меньше единицы, то происходит убыль потока, если больше единицы - поток увеличивается.

Алгоритм находит искомые значения потоков, втекающих в дугу, искомые значения потоков, вытекающих из дуги, максимальный поток, втекающий в узел - исток, и вытекающий из узла - истока поток.

Пример использования алгоритма: оросительная система с фильтрацией и испарением, задачи на неучтенные потери и брак при производстве.