Теорема сложения вероятностей. Противоположные события. Условные вероятности. Теорема умножения вероятностей. Независимые события. Вероятность появления хотя бы одного события.

 

Теорема 2.1 (теорема сложения).Вероятность р(А + В) суммы событий А и В равна

Р (А + В ) = р (А) + р (В) – р (АВ). (2.2)

Доказательство.

Докажем теорему сложения для схемы случаев. Пусть п – число возможных исходов опыта, т_А – число исходов, благоприятных событию А, т_В – число исходов, благопри-ятных событию В, а т_АВ – число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ). Тогда число исходов, при которых имеет место событие А + В, равно т_А + т_В – т_АВ (так как в сумме (т_А + т_В) т_АВ учтено дважды: как исходы, благоприятные А, и исходы, благоприятные В). Следовательно, вероятность суммы можно определить по формуле (1.1):

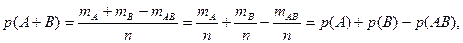
что и требовалось доказать.

 

Следствие 1. Теорему 2.1 можно распространить на случай суммы любого числа событий. Например, для суммы трех событий А, В и С

Р(А + В + С) = р(А) + р(В) + р(С) – р(АВ) – р(АС) – р(ВС) + р(АВС) (2.3)

и т.д.

 

Следствие 2. Если события А и В несовместны, то т_АВ = 0, и, следовательно, вероятность суммы несовместных событий равна сумме их вероятностей:

Р(А + В) = р(А) + р(В). (2.4)

 

Определение 2.1. Противоположными событиями называют два несовместных события, образующих полную группу. Если одно из них назвать А, то второе принято обозначать .

Замечание. Таким образом, заключается в том, что событие А не произошло.

 

Теорема 2.2. Сумма вероятностей противоположных событий равна 1:

р(А) + р() = 1. (2.5)

 

Доказательство.

Так как А и образуют полную группу, то одно из них обязательно произойдет в результате опыта, то есть событие А +является достоверным. Следовательно,

Р( А +) = 1. Но, так как А инесовместны, из (2.4) следует, что Р(А +) = р(А) + р(). Значит, р(А) + р() = 1, что и требовалось доказать.

 

Замечание. В ряде задач проще искать не вероятность заданного события, а вероятность события, противоположного ему, а затем найти требуемую вероятность по формуле (2.5).

 

Пример. Из урны, содержащей 2 белых и 6 черных шаров, случайным образом извлека-ются 5 шаров. Найти вероятность того, что вынуты шары разных цветов.

Решение. Событие, противоположное заданному, заключается в том, что из урны вынуто 5 шаров одного цвета, а так как белых шаров в ней всего два, то этот цвет может быть только черным. Множество возможных исходов опыта найдем по формуле (1.5):

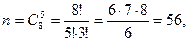
а множество исходов, благоприятных событию - это число возможных наборов по 5 шаров только из шести черных:

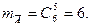
Тогда а