ГЛАВА 1. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И СТАНДАРТНОГО ОТКЛОНЕНИЯ ДЛЯ ОЦЕНКИ РИСКА

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ

 

 

ЭКОНОМЕТРИКА

 

Методические указания для выполнения контрольной работы и подготовке к зачету для студентов заочной формы обучения

 

Специальность: 080109 - Бухгалтерский учет, анализ и аудит

 

 

Москва


ОГЛАВЛЕНИЕ

ГЛАВА 1. Применение математического ожидания и стандартного

Отклонения для оценки риска стр. 3

ГЛАВА 2. Линейная регрессия стр. 5

1. Простая модель линейной регрессии стр. 5

2. Ошибки стр. 7

3. Коэффициент корреляции Пирсона. Коэффициент детерминации стр. 7

4. Предсказания и прогнозы на основе модели линейной регрес­сии стр. 10

5. Основные предпосылки в модели парной линейной регрессии стр. 11

6. Процедура испытания гипотез стр. 11

7. Испытание гипотезы для оценки линейности связи стр. 13

8. Доверительные интервалы в линейном регрессионном анализе стр. 16

9. Регрессия и MS Excel стр. 17

ГЛАВА 3. Временные ряды стр. 20

1. Анализ аддитивной модели стр. 22

2. Анализ мультипликативной модели стр. 26

3. Преимущества и недостатки метода скользящей средней стр. 29

 

Список вопросов для зачета стр. 33


ГЛАВА 1. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И СТАНДАРТНОГО ОТКЛОНЕНИЯ ДЛЯ ОЦЕНКИ РИСКА

 

Сравниваются варианты инвестирования, для которых известны возможные значения прибыли х1, ..., xn, а также вероятности p1, ..., pn получения данной прибыли соответственно.

Для каждого варианта вычисляются математическое ожидание 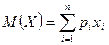(характеризует среднюю прибыль) и стандартное отклонение 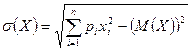(это оценка риска проекта).

 

Пример 1.В таблице указаны вероятности получения прибыли для двух вариантов инвестирования. Сравним эти варианты.

Прибыль, млн. руб. -2 -1
Вариант 1 0,1 0,1 0,3 0,2 0,3
Вариант 2 0,1 0,2 0,1 0,2 0,2 0,2

 

Прибыль Вариант 1 Вариант 2
p px px2 p px px2
-2 0,1 -0,2 0,4 0,1 -0,2 0,4
-1 0,1 -0,1 0,1 0,2 -0,2 0,2
0,3 0,1
0,2 0,2 0,2 0,2 0,2 0,2
0,3 0,6 1,2 0,2 0,4 0,8
0,2 0,6 1,8
Сумма 0,5 1,9 0,8 3,4

Поясним, как заполняется таблица. Числа из 1-й, 2-й и 3-й строк исходной таблицы запишем в 1-м, 2-м и 5-м столбцах новой таблицы соответственно. 3-й (6-й) столбец равен произведению 1-го и 2-го (5-го) столбцов. Числа 3-го (6-го) столбца умножаем на числа 1-го столбца и результат пишем в 4-м (7-м) столбце. В последней строке указаны суммы элементов соответствующих столбцов.

Для 1-го варианта математическое ожидание M(X) и стандартное отклонение σ(X) равны:

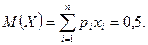
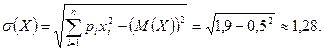
Для 2-го варианта математическое ожидание M(X) и стандартное отклонение σ(X) равны:

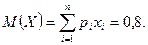
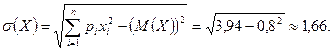
Мы видим, что во 2-м варианте средняя прибыль выше, но и оценка риска во 2-м варианте больше. Инвестор, склонный к риску, предпо­чтет 2-й вариант. Более осторожный инвестор ограничится 1-м вари­антом.

То, что стандартное отклонение является мерой риска, многими воспринимается как аксиома. Но этот показатель не всегда точно от­ражает действительность. Ожидаемые доходы, как правило, оцени­ваются с помощью прошлых доходов. При значительном изменении со временем активов предприятия прогнозы, полученные на основа­нии данных прошлых лет, будут совершенно бесполезными при оценке риска.

Инвесторы при принятии решений ориентируются на ожидае­мую доходность инвестиций. При хороших перспективах роста Предприятия можно ожидать и высоких доходов. Но высокий доход связан с высоким риском. Поэтому следует обратить особое внимание на такие факторы, как общее состояние экономики, отрасль экономики и показатели конкретного предприятия.