СОДЕРЖАНИЕ

Э 40

Печатается по решению редакционно-издательского совета

Муромского института (филиала)

Владимирского государственного университета имени Александра Григорьевича

и Николая Григорьевича Столетовых

Э 40 Эконометрика:метод. указания к практическим занятиям по дисциплине Эконометрика для студентов образовательной программы / сост.: А.И. Мосалёв. – Муром: Изд.-полиграфический центр МИ ВлГУ, 2010. - с.

Содержит основной материал практического применения инструментов эконометрики для исследования экономических процессов и явлений с целью дальнейшего анализа возможных событий в будущем. Приведены варианты решения задач, а также представлен материал для самостоятельного решения.

УДК 330.43(07)

ББК 65в631я7

государственного образовательного учреждения

высшего профессионального образования

«Владимирский государственный университет», 2012

СОДЕРЖАНИЕ

ПАРНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ

ЗАДАНИЯ ПО ВАРИАНТАМ

Вопросы для рассмотрения

Практическая часть

ЛИТЕРАТУРА

ПРИЛОЖЕНИЯ

№ 1. ПАРНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ

Существуют два варианта взаимосвязи между переменными x и y:

1. х и у равноценные, при этом основным является вопрос по наличии и силе взаимосвязи между Х и У.

Например Х – доходность акций, У – доходность облигаций.

Х – доходность ПИФа, У – доходность обезличенного вклада.

При исследовании зависимости между такими переменными используется корреляционный анализ, основная мера которого

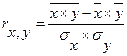
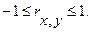
Если r_x_,_y = -1, то x и y связаны отрицательной линейной зависимостью. Если r_x_,_y =1, то х и у связаны положительной линейной зависимостью. Если r_x_,_y =0, то между х и у отсутствует связь.

2. Х и У связаны зависимостью. Если х – независимая переменная, а У – зависимая переменная, тогда изменение Х обязательно влечёт изменение У.

Например: Х – доход компании, У – вкладывание средств в активы предприятия, тогда Х↑→У↑.

Х – цена, У – спрос, тогда Х↑→У↓.

Х – курс волют, У – объём чистого экспорта: Х↓→У↓.

Однако, такие зависимости неоднозначные, так как каждому конкретному значению объясняющей переменной Х соответствует некоторое вероятностное распределение зависимой переменной У, поэтому анализируется, как переменная Х влияет на среднее значение зависимой переменной.

- такая зависимость называется функцией регрессии Y на Х.

Регрессия – это функциональная зависимость между объясняющими переменными и условным математическим ожиданием зависимой переменной, которая строится с целью прогнозирования этого среднего значения при фиксированных значениях объясняющей переменной.

В регрессионных моделях обязательно включаются случайная переменная ε, определяющая случайный характер регрессионной связи,

Причины наличия ε в регрессионных уравнениях:

- не включение в модель всех объясняющих переменных;

- неправильный выбор функциональной формы модели;

- агрегирование переменных (т.е. в зависимости используются факторы, которые сами являются сложными комбинациями более простых переменных, например совокупный спрос, как комбинация индивидуальных спросов);

- ошибки измерений;

- ограниченность статистических данных;

- непредсказуемость человеческого фактора – эта причина может испортить самую качественную модель, так как невозможно спрогнозировать поведение каждого отдельного человека.

Этапы построение регрессионной модели:

1. этап спецификации – в случае парной регрессии выбор формулы осуществляется по графическому изображению реальных статистических данных в виде точек в декартовой системе координат, которая называется корреляционной формой или диаграммой рассеивания.

x_i	x₁	x₂	…	x_n
y_i	y₁	y₂	…	y_n

рисунок 1. рисунок 2. рисунок 3

return false">ссылка скрыта

рисунок 4. рисунок 5. рисунок 6.

рисунок 7.

рисунок 1 – связь близка к линейной, поэтому функцию регрессии выбираем в виде ;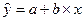

рисунок 2 - - параболическая зависимость (полином второго порядка);

рисунок 3 – явная взаимосвязь между х и у отсутствует, поэтому какую бы ни выбрали форму связи, результат спецификации и параметризации будет неудачным;

рисунок 4 – зависимость описывается уравнением равносторонней гиперболы ;

рисунок 5 – связь с логлинейным распределением (степенное уравнение парной регрессии) ;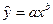

рисунок 6 – связь описывается показательным уравнением ;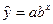

рисунок 7 – представлен полином третьего порядка, уравнение которого выглядит следующим образом

Существуют и другие уравнения, описывающие однофакторную регрессионную зависимость. Среди них выделяются:

1) экспоненциальное уравнение бывает двух видов:

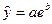
2) логарифмическое (полулогарифмическое) уравнение парной регрессии:

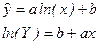
3) обратное уравнение парной регрессии

2. Этап параметризации – находятся численные значения параметров регрессии функции a, b, c, при использовании метода наименьших квадратов;

3. Этап верификации – проверяется качество найденных параметров: оценивается их точность, статистическая значимость, находятся их доверительные интервалы, а также оценивается общее качество уравнения регрессии по численному значению коэффициента детерминации.

Для решения задач в эконометрике используется метод наименьших квадратов, суть которого заключается в определении оценок предложенного уравнения регрессии.

Для работы с регрессионным анализом следует проводить следующие шаги: