Раздел 2. ОСНОВНЫЕ ПОНЯТИЯ ЭКОНОМЕТРИКИ

 

Эконометрика – наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов.

Эконометрика – это дисциплина, объединяющая совокупность теоретических результатов, методов и приемов, позволяющих на базе экономической теории, экономической статистики и математико-статистического инструментария получать количественное выражение качественным закономерностям. Курс эконометрики призван научить различным способам выражения связей и закономерностей, через эконометрические модели и методы проверки их адекватности, основанные на данных наблюдений. От математико-статистического, эконометрический подход отличается тем вниманием, которое уделяется в нем вопросу соответствия выбранной модели изучаемому объекту, рассмотрению причин, приводящих к необходимости пересмотра модели на основе более точной системы представлений.

Эконометрика занимается, по существу, статистическими выводами, т.е. использованием выборочной информации для получения некоторого представления о свойствах генеральной совокупности. Наиболее распространенными эконометрическими моделями, являются производственные функции и модели, описываемые системой одновременных уравнений.

Метод наименьших квадратов – традиционный метод, используемый для составления функциональной зависимости. Предполагает минимизацию квадратов отклонений значений результирующего фактора, рассчитанного с помощью функции от его фактического значения.

Корреляционный анализ – является одним из методов эконометрического анализа взаимозависимости нескольких признаков. Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке и определении на ее основе оценок частных и множественных коэффициентов корреляции и детерминации.

Парный коэффициент корреляции характеризует тесноту линейной зависимости между двумя переменными:

Его значения изменяются в пределах от -1 до 1, причем, чем ближе значение коэффициента по абсолютной величине к единице, тем сильнее

 

 

зависимость между переменными. В табл. 2 представлена оценка тесноты линейной связи с помощью коэффициента корреляции (r).

Таблица 2

Оценка тесноты линейной связи

Значение	Теснота линейной связи
0 – 0,1	Связь отсутствует
0,1 – 0,3	Слабая
0,3 – 0,5	Умеренная
0,5 – 0,7	Заметная
0,7 – 0,9	Высокая
0,9 – 0,99	Очень высокая
	Функциональная

При r > 0 связь прямая, т.е. с ростом х растет у.

При r < 0 связь обратная, т.е. с ростом х убывает у.

 

Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной (результативной) и остальными, входящими в модель.

Значимость коэффициентов корреляции проверяется по t-критерию Стьюдента. Наблюдаемое (фактическое) значение находится по формуле:

где r – значение частного или парного коэффициента корреляции;

l – порядок частного коэффициента корреляции, т.е. число фиксированных факторов. Для парного коэффициента корреляции l = 0.

Найденное значение сравнивается с табличным (приложение 1). Если t_факт > t_табл, то линейный коэффициент корреляции значим и существует связь между показателями х и у.

Квадрат коэффициента корреляции – коэффициент детерминации. Он показывает какая доля изменений результативного признака обусловлена изменением показателя х.

Регрессионный анализ – это статистический метод исследования зависимости случайной величины Y от переменных X_j (j = 1; k), рассматриваемых в регрессионном анализе как неслучайные величины

 

 

,

где – средние квадратические отклонения

;

.

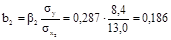Параметр определим из соотношения:

.

Получим уравнение:

.

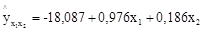Каждый из коэффициентов уравнения регрессии определяет среднее изменение урожайности за счет изменения соответствующих факторов и фиксированного уровня другого так, коэффициент при х₁ показывает, что увеличение (или снижение) количества внесения удобрений на 1 ц ведет к повышению (или снижению) урожайности зерновых на 0,976 ц. Соответственно коэффициент при х₂ определяет меру зависимости урожайности зерновых от насыщенности севооборота.

return false">ссылка скрыта

1.Для определения линейного коэффициента множественной корреляции используем формулу:

Коэффициент множественной корреляции показывает наличие зависимости (связь умеренная) между анализируемыми признаками. Коэффициент множественной детерминации = 0,495² = 0,245 свидетельствует, что 24,5% изменения урожайности зерновых связано с анализируемыми признаками.

3. Для проверки статистической значимости (существенности) множественного коэффициента корреляции рассчитаем t-критерий Стьюдента по формуле: