Необходимо определить средний квартальный коэффициент роста выпуска продукции.
Например, имеются следующие данные о выпуске продукции по кварталам отчетного года.
Средняя геометрическая применяется для исчисления среднего коэффициента роста в рядах динамики.
Средние показатели могут рассчитываться по дискретным и интервальным вариационным рядам. При этом расчет производится по средней арифметической взвешенной. Для дискретного ряда данная формула используется так же, как и в приведенном выше примере. В интервальном же ряду для расчета определяются середины интервалов.
В качестве веса в этой задаче был принят показатель общих затрат времени на изготовление всех деталей одним рабочим. Т.к. затраты времени у всех одинаковые, то к аналогичному результату приходим выполняя расчет по формуле средней гармонической простой
| Показатель | Кварталы года | |||
| I | II | III | IV | |
| Выпуск продукции (в тыс. руб.) | ||||
| Условные обозначения | y0 | y1 | y2 | y3 |
| Коэффициент роста (снижения) выпуска продукции по сравнению с предыдущим кварталом | - | 1.2 | 1.04 | 0.976 |
| Условные обозначения | K1=y1/y0 | K2=y2/y1 | K3=y3/y2 |
Формула средней геометрической простой применяется для расчета среднего коэффициента роста, если промежутки времени, к которым относятся коэффициенты роста, одинаковы.
Средняя арифметическая обладает рядом свойств:
1. Сумма отклонений индивидуальных значений признака от их средней величины равна 0; 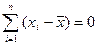
2. От уменьшения (или увеличения) частот каждого значения признака х в n раз величина средней арифметической не изменится 
3. Общий множитель индивидуального значения признака может быть вынесен за знак средней:
