Анализ устойчивости по корням характеристического уравнения системы
ГЛАВА 7. Устойчивость линейных систем автоматического регулирования (управления)
Процесс регулирования может быть сходящимся (регулируемый параметр стремится к положению равновесия) или расходящимся (регулируемый параметр все время уходит от положения равновесия). Колебательные процессы могут быть затухающими (сходящимися), незатухающими (колебания с постоянной амплитудой) и расходящимися.
Ясно, что системы, в которых возникают расходящиеся процессы (чаще всего колебательные), являются неработоспособными. Они приводят к нарушению хода технологического процесса, что может вызвать аварии, для предотвращения которых срабатывает аварийная защита. Для описания характеристик отмеченных особенностей поведения систем регулирования введено понятие «устойчивость».
Устойчивость автоматической системы – это свойство системы возвращаться в исходное состояние равновесия после прекращения возмущения, выведшего систему из этого состояния. Неустойчивая система не возвращается в исходное состояние, а непрерывно удаляется от него.
Сущность устойчивости, неустойчивости и виды процессов (апериодический или колебательный) определяется характером свободного движения системы.
Дифференциальное уравнение свободного движения линейной системы автоматического управления, записанное в операторном виде, для свободной составляющей регулируемой величины jсв(t), имеет вид
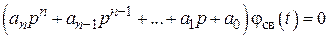. (7.1)
Вынужденная составляющая регулируемой величины, зависящая от вида внешнего возмущения и правой части уравнения системы регулирования, на устойчивость системы не влияет.
Система будет устойчивой, если свободная составляющая jсв(t) переходного процесса с течением времени стремится к нулю:
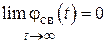. (7.2)
Тогда выходная величина с течением времени будет стремиться к вынужденной составляющей. Устойчивость по (7.2) принято называть асимптотической устойчивостью.
Если свободная составляющая с течением времени неограниченно растет, т.е.
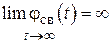, (7.3)
то система неустойчива.
Если свободная составляющая jсв(t) не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости.
Рассмотрим эти случаи качественно на примере полученного ранее уравнения системы, составленного для внешнего возмущения l.
Уравнение вынужденного движения системы
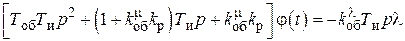. (7.4)
Решением уравнения является сумма двух составляющих
,
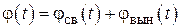где jсв(t) – свободная составляющая, получаемая из решения уравнения свободного движения системы, а jвын(t) – вынужденная составляющая, получаемая из уравнения вынужденного движения системы (7.4).
Уравнение свободного движения системы
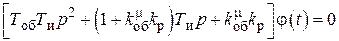. (7.5)
Решением уравнения (7.5) является сумма экспонент
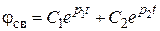, (7.6)
где р1 и р2 – корни характеристического уравнения системы; С1 и С2 – постоянные коэффициенты, зависящие от начальных условий.
Характеристическое уравнение системы
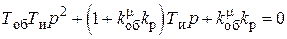. (7.7)
Запишем это уравнение в более удобном виде (как при рассмотрении инерционного звена второго порядка):
. (7.8)
Здесь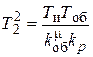 
; 
.
Уравнение имеет два корня р1 и р2:
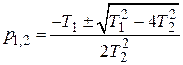, (7.9)
где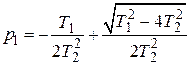 
; 
.
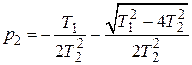Все случаи устойчивости зависят от вида корней характеристического уравнения: они могут быть действительными числами или комплексно-сопряженными числами. Если корни характеристического уравнения –действительные числа, то процесс будет апериодическим, а при комплексных числах – колебательным.
Рассмотрим эти случаи.
1. Корни характеристического уравнения р1 и р2 – действительные числа.
Они получаются, если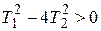 
в подкоренном выражении, т.е. 
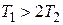. При этом соотношения коэффициентов получаем действительные корни. Они в общем случае могут быть положительными или отрицательными: р1,2 > 0; р1,2 < 0:
а) при р1,2 < 0 экспоненты с отрицательными показателям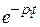и 
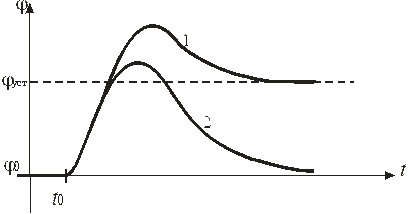
и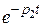 
в уравнении (7.6) с течением времени t стремятся к нулю, следовательно, свободная составляющая jсв(t) стремится к нулю. Система будет устойчивой, процесс регулирования – апериодическим (рис. 7.1);
| Рис. 7.1. Процесс апериодический: 1 – статическая система (П-закон); 2 – астатическая система (ПИ-, ПИД-законы). Процессы апериодические (неколебательные). Системы устойчивы. |
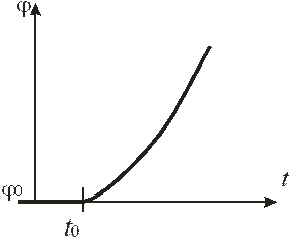
б) при р1,2 > 0 экспоненты с положительным показателем с течением времени будут стремиться к бесконечности, следовательно, свободная составляющая регулируемого параметра jсв(t) также стремится к бесконечности. Процесс будет апериодическим, система неустойчива (рис. 7.2).
| Рис. 7.2. Процесс апериодический. Система неустойчива. |
2. Корни характеристического уравнения р1 и р2 – комплексные числа (колмплексно-сопряженные).
Они получаются при Т1< 2Т2. Тогда подкоренное выражение 
<0.
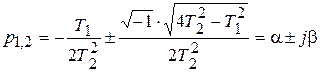, (7.10)
где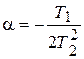 
; 
; 
.
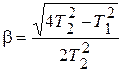Решение дифференциального уравнения опять зависит от экспоненты при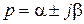 
:
.
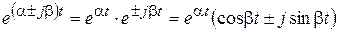Наличие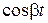 
и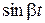 
говорит о том, что процесс регулирования будет колебательным, а еat определяет амплитуду колебаний. Следовательно, рост или затухание амплитуды колебаний с течением времени зависит от того, больше или меньше нуля действительная часть a комплексного числа:
а) a<0,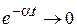 
. С течением времени колебания затухают. Система устойчива (рис. 7.3).
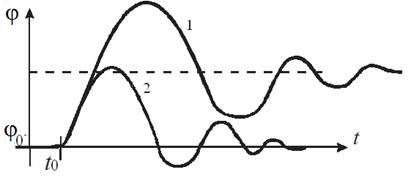
| Рис. 7.3. Колебательный процесс регулирования: 1 – П, ПД-законы; 2 – ПИ, ПИД-законы Системы устойчивы |
б) a>0,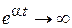 
. С течением времени амплитуда колебаний растет. Система неустойчива (рис. 7.4).
Если поведение системы описывается дифференциальным уравнением высокого порядка, то общее решение также представлено в виде суммы экспонент:
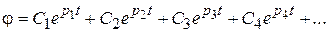
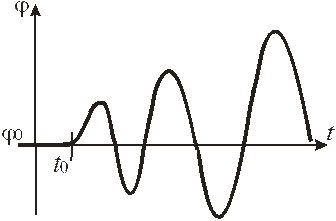
| Рис. 7.4. Колебательный процесс регулирования. Система неустойчива. |
Все предыдущие рассуждения имеют силу и в этом случае, только для всех корней р1, р2, р3, р4, ….
Общее условие устойчивости по корням характеристического уравнения системы:
| Для того, чтобы система автоматического регулирования была устойчивой, необходимо и достаточно, чтобы все действительные корни характеристического уравнения системы и все действительные части комплексно-сопряженных корней были отрицательны. Если, хотя бы один из действительных корней или действительная часть одного комплексно-сопряженного корня будут положительны, система будет неустойчивой. |
3.Если действительная часть комплексно-сопряженных корней равна нулю (a=0), система находится на границе устойчивости.
Действительно, тогда
.
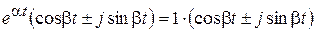Система совершает колебания с постоянной амплитудой.
Таким образом, устойчивость системы зависит только от вида корней характеристического уравнения и не зависит от характера внешних воздействий на систему. Устойчивость – это внутренне свойство системы, присущее ей вне зависимости от внешних воздействий.
Если система описывается дифференциальным уравнением высокого порядка, то определить его корни решением уравнения невозможно. В теории автоматического регулирования (управления) разработан ряд правил, с помощью которых можно судить о знаках корней, не решая характеристического уравнения и не находя числовых значений самих корней. Эти правила называются критериями устойчивости.
Критерии устойчивости могут быть алгебраическими и частотными.
Алгебраические критерии устанавливают необходимые и достаточные условия отрицательности корней характеристического уравнения в форме ограничений, накладываемых на определенные комбинации коэффициентов характеристического уравнения.
Частотные критерии определяют связь между устойчивостью системы и формой частотных характеристик системы. Наиболее распространенными в инженерной практике являются алгебраический критерий устойчивости Гурвица и частотные критерии устойчивости Михайлова и Найквиста.